Реферат: История тригонометрии в формулах и аксиомах
а
А b С 0,620°M Рис.3.
Радиусы АМ и АN разделим на 100 равных частей. Построим прямоугольный треугольник с вершиной в центре круга и катетом совпадающим с радиусом АМ и гипотенузой АВ =1. Если угол ВАС =a, то по определению тригонометрических функций мы имеем:
sin a=а
Для угла 52° на шкале радиуса АN находим, что а =0,79, а на шкале радиуса АМ находим, что b =0,62., то есть sin 52°=0,79.
Построив прямоугольные треугольники для углов a=2°, 4°, 6°, 8°,…, 88°, согласно рис.3., найдем значения (при аккуратных измерениях и вычислениях) с точностью до 0,01. Для углов 0°и 90°прямоугольных треугольников не существует. Однако, если гипотенуза АВ будет стремиться по положению к радиусу АМ , то угол a®0, а катеты а ®0 и b ®1. В таком случае для полноты значений тригонометрических функций принимают, что
sin 0°=а =0; cos 0°=b =1.
![]()
![]()
![]()
![]()
![]() Что касается значений tg a и ctg a, то при a®0 отношение ®0, т.е. , а отношение при a®0 неограниченно возрастает. Этот результат записывают как ®¥, где символ ¥ указывает, что величина неограниченно возрастает и не может быть выражена никаким числом, так как знак ¥ не является каким-либо числом. Таким образом, принимают, что tg 0°=0, а ctg 0°не существует, что чаще записывают какctg 0°=¥.
Что касается значений tg a и ctg a, то при a®0 отношение ®0, т.е. , а отношение при a®0 неограниченно возрастает. Этот результат записывают как ®¥, где символ ¥ указывает, что величина неограниченно возрастает и не может быть выражена никаким числом, так как знак ¥ не является каким-либо числом. Таким образом, принимают, что tg 0°=0, а ctg 0°не существует, что чаще записывают какctg 0°=¥.
Рассуждая аналогично при a®90° приходим к целесообразности принять что
sin 90°=1; cos 90°=0, tg 90° не существует (tg 90°®¥) и ctg 90°=0.
Приведем таблицу значений синусов для углов от 0° до 90° с шагом 2°, которую можно получить указанным выше способом.
| градусы | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| sin | 0,00 | 0,03 | 0,07 | 0,10 | 0,14 | 0,17 | 0,21 | 0,24 | 0,28 | 0,31 | 0,34 | 0,37 |
| градусы | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 |
| sin | 0,41 | 0,44 | 0,47 | 0,50 | 0,53 | 0,56 | 0,59 | 0,62 | 0,64 | 0,67 | 0,69 | 0,72 |
| градусы | 48 | 50 | 52 | 54 | 56 | 68 | 60 | 62 | 64 | 66 | 68 | 70 |
| sin | 0,74 | 0,77 | 0,79 | 0,81 | 0,83 | 0,93 | 0,87 | 0,88 | 0,90 | 0,91 | 0,93 | 0,94 |
| градусы | 72 | 74 | 76 | 78 | 80 | 82 | 84 | 86 | 88 | 90 | ||
| sin | 0,95 | 0,96 | 0,97 | 0,98 | 0,98 | 0,99 | 0,99 | 1,00 | 1,00 | 1,00 |
Пользуясь значениями тригонометрической функции y =sinx из таблицы, построим график.
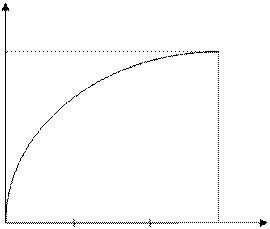 y
y
|
1
0 30° 60° 90°x
Рис.4.
Основные соотношения между тригонометрическими функциями острого угла
Для прямоугольного треугольника в соответствии с теоремой Пифагора
a2 +b2 =c2
![]() или
или
По определению тогда
(1)
Легко также найти следующие зависимости
(2)
![]() (3)
(3)
(4)
(5)
![]() Из соотношений (1)-(5), которые называют основными, можно вывести и другие вспомогательные соотношения, например:
Из соотношений (1)-(5), которые называют основными, можно вывести и другие вспомогательные соотношения, например:
![]() (6)
(6)
![]() (7)
(7)
(8)