Реферат: Измерение характеристик случайных сигналов

Статистические измерения – это методы и средства измерения параметров и характеристик случайных сигналов. Они базируются на общих принципах измерений параметров сигналов, но имеют свою специфику и особенности, вытекающие из теории случайных процессов.

Вероятностные характеристики случайных сигналов

Случайным называется сигнал, мгновенные значения которого изменяются во времени случайным образом. Он описывается случайной функцией времени Х(t). Эту функцию можно рассматривать как бесконечную совокупность функций x_i (t), каждая из которых представляет собой одну из возможных реализаций X(t). Графически это можно представить следующим образом (рисунок 1):

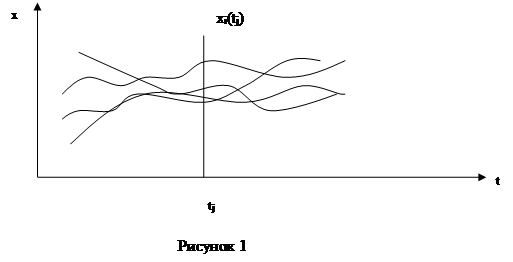Полное описание случайных сигналов может быть произведено с помощью системы вероятностных характеристик. Любая из этих характеристик может быть определена либо усреднением по совокупности реализации x_i (t), либо усреднением по времени одной бесконечно длинной реализации.

Зависимость или независимость результатов таких усреднений определяет следующие фундаментальные свойства случайных сигналов – стационарность и эргодичность.

Стационарным называется сигнал, вероятностные характеристики которого не зависят от времени.

Эргодическим называется сигнал, вероятностные характеристики которого не зависят от номера реализации.

Для стационарных эргодических сигналов усреднение любой вероятностной характеристики по множеству реализаций эквивалентно усреднению по времени одной теоретически бесконечно длинной реализации.

Для практических целей наиболее важными являются следующие вероятностные характеристики стационарных эргодических сигналов, имеющих длительность реализации Т:

- среднее значение (математическое ожидание). Оно характеризует постоянную составляющую сигнала

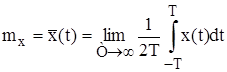; (1)

- средняя мощность. Она характеризует средний уровень сигнала

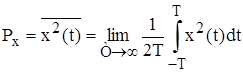; (2)

- дисперсия, характеризующая среднюю мощность переменной составляющей сигнала:

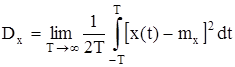; (3)

- среднеквадратическое отклонение (СКО)

; (4)

- функция распределения, которая определяется как интегральная вероятность того, что значение xi(tj) в j-й момент времени будут ниже некоторых значений X:

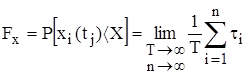. (5)

Для заданных стационарных эргодичных сигналов F_x характеризуется относительным временем пребывания реализации ниже уровня Х (τ_i –, i –й интервал пребывания, n – количество интервалов, рисунок 2)

- одномерная плотность вероятности, называемая дифференциальным законом распределения:

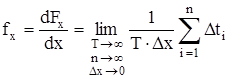, (6)

где - расстояние между соседними уровнями X(t), называемое дифференциальным коридором;

- i – й интервал пребывания реализации в пределах (см. рисунок 1.11).

- корреляционная функция. Она характеризует стохастическую (случайную) связь между двумя мгновенными значениями случайного сигнала, разделенного заданным интервалом времени τ

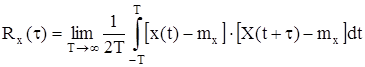; (7)

- взаимная корреляционная функция. Она характеризует стохастическую связь мгновенными значениями случайных сигналов x(t) и y(t), разделенными интервалом времени τ

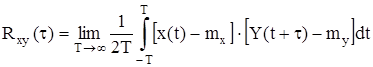. (8)

Из выражений (1)-(8) видно, что все вероятностные характеристики представляют собой неслучайные числа или функции и определяется по одной реализации бесконечной длительности. Практически же длительность Т, называемая продолжительностью анализа, всегда ограничена, поэтому на практике мы можем определить не сами характеристики, а только их оценки. Эти оценки, полученные экспериментальным путем, называются статическими характеристиками. А раз оценка, значит приближение, которое характеризуется погрешностями, называемыми статистическими погрешностями.

Измерение среднего значения средней мощности и дисперсии

Согласно формуле (1) измерение m_x сводится к интегрированию случайного сигнала за время Т. Интегрирование можно выполнить с помощью анало-

--> ЧИТАТЬ ПОЛНОСТЬЮ <--