Реферат: Изоморфизм уравнений диссипативных свойств растворов электролитов

R0 – радиус молекулы растворителя,

р – дипольный момент молекулы растворителя,

 - диэлектрическая проницаемость среды,

Мs – молекулярная масса растворителя.

Zэ – экранированный заряд ядра находится используя константы экранирования Слейтера  определяемые по стандартным правилам приводимым в различных учебниках по теоретической основе неорганической химии, в частности [9].

Таблица 1

Радиусы ионов, сольватные числа и радиусы сольватированных ионов рассчитанные по уравнениям 26 – 28

Ион	I, эв	Zэ		ns
Li+	75,62	2,7	0,5446	7,3873	4,4246
Na+	47,29	6,55	1,0004	3,2301	3,3583
K+	31,81	7,75	1,3785	1,8682	2,7980
Cl-	3,82	4,875	1,8100	1,0090	2,2786

Таблица 2

Приведенные радиусы молекул рассчитанные по формуле 25

Молекула
LiCl	1,5040
NaCl	1,3575
KCl	1,2559

Выражая из уравнения (17) вязкость и коэффициент диффузии через электропроводность (Т = 298К), получим отдельно для каждого i-го иона:

(29)

(30)

Переходя к вязкости и диффузии, как свойствам раствора, необходимо учитывать взаимную корреляцию движения ионов противоположного знака, поэтому вязкости и коэффициенты диффузии отдельных ионов одной молекулы, объединяем в приведенное значение.

Например, для 1-1 электролита

(31)

(32)

Соответственно при бесконечном разбавлении

(33)

(34)

Неренст и Хартли для определения коэффициента диффузии одного единственного электролита предложили уравнение (23)

(35)

где D0 – предельное значение коэффициента диффузии по Нернсту (33)

Сравнивая теоретические уравнения электропроводности (1) и диффузии по Неренсту – Хартли (35), учтя в последнем максвеловское распределение по скоростям и параметр экранирования, можно показать, что

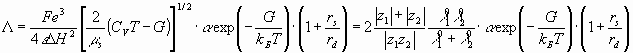(36, 37)

Электропроводности экспериментально найденные, и рассчитанные по уравнениям (36, 37), приведены в таб. 4.3 – 4.5.

Из полученных данных можно сделать вывод, что электропроводность найденная по уравнению (36) хорошо согласуется с экспериментально найденной в случаях хлоридов натрия и калия, хуже для хлорида лития, но электропроводность рассчитанная по уравнению (37) для хлорида лития практически совпадает с данными полученными по уравнению (36), в остальных случаях уравнение (37) дает небольшое расхождение с опытом.

Роль среднего значения кинетической энергии ионов в уравнении (1), которая, согласно теореме вариала, равна по модулю среднему значению полной энергии, играет функция 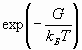, причем 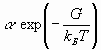- есть максвелловское распределение по скоростям.

В уравнении (35) выражение равно , а это есть –полная энергия молекулы при данной концентрации.

Роль распределения для коэффициента диффузии играет функция , которую, если учесть  при средне молярном коэффициенте активности, можно представить в виде 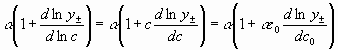.