Реферат: Изучение механизмов металлорежущих станков

4) четырехмерные , R=4 (например пространственные рычажно-винтовые и кулачковые механизмы;

5) пятимерные , R=5 (например пространственные шарнирно-рычажные, кулачковые и зубчато-рычажные механизмы);

6) шестимерные , R=6 (например пространственные шарнирно-рычажные, кулачковые и зубчато-рычажные механизмы)

4.3. Подвижность W механизма. Она определяется числом степеней свободы движений в механизме, т.е. числом независимых движений на разных входных звеньях, передающих их на одно выходное звено механизма. В соответствии с этим механизмы могут быть одноподвижными (подавляющее большинство) и многоподвижными . Примерами последних являются разнообразные суммирующие механизмы станков ([3], стр.79) и промышленные роботы. Подвижность всего механизма зависит от подвижностей отдельных кинематических пар (j;k), определяемых числом возможных перемещений одного звена пары относительно другого. Могут быть одно-, двух-,…, пятиподвижные кинематические пары (табл.2).

В сложном передаточном механизме общая подвижность определяется следующим выражением:

(4)

где - суммарная подвижность всех р кинематических пар механизма, ;

R_å - сумма размерностей N простых механизмов, входящих в состав сложного, R_å = R₁ + R₂ +…+ R_N ;

v_п – число местных избыточных (пассивных) подвижностей в кинематических парах. Например, лишняя подвижность в паре Р₁₂ (рис.1а) или «лишнее» вращение ролика 2 (рис.3) на рычажном толкателе 3, не влияют на положение и движение других звеньев механизма. Избыточные подвижности применяют для уменьшения трения, для компенсации перекосов и других погрешностей с целью повышения работоспособности механизмов.

с_к - число жестких кинематических связей в сложном механизме. К числу кинематических связей относятся как отдельные дополнительные звенья (рычаги, кулачки, шестерни и т.п.), так и цепи дополнительных механизмов, дублирующих или дополняющих работу основных передач. Указанные кинематические связи образуют замкнутые механические контуры (замкнутые механизмы) и способствуют повышению точности, жесткости и других свойств механизмов. Примерами простейших кинематических связей являются дополнительные шатун 4 (рис.1б) и сателлит 7 (рис.5). Пример более сложной кинематической связи показан на рис.1г. Здесь от двигателя М с помощью зубчатой пары z₁ /z₂ на вал 2 передается вращение, которое затем разделяется на два потока передачами z₃ /z₄ , z₅ /z₆ и z₇ /z_{8 ,} z₉ /z₁₀ , замыкаясь с помощью шестерен z₁₁ и z₁₂ на зубчатой рейке, закрепленной на столе станка. Усилие Q гидроцилиндра или мощной пружины 3 на вал2, благодаря косозубым зацеплениям шестерен, создает дополнительный натяг между боковыми поверхностями зубьев колес z₁₁ , z₁₂ с рейкой. В этом механизме n=7, p=14, N=7, с_к =1 (один замкнутый контур), v_п =0 и W = ( 14 + 7 ) + 1 – 7 × 3 = 1 (все простые механизмы – трехмерные, R_j =3 ).

Подвижность простого механизма в соответствии с (4) равна:

W = v_S - R_j - v_п (5)

Здесь с_к =0, т.к. введение кинематических связей в простой механизм делает его сложным. Например, присоединение дополнительного шатуна 4 (рис. 1б) в шарнирный четырехзвенник добавляет в него две кинематические пары, поэтому N = 6 – 4 = 2 (два подобных четырехзвенника).

5. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА МЕХАНИЗМОВ.

5.1. Трансформизм . Он характеризуется передаточным отношением i ₁₂ , равным производной от параметра положения (j₂ , S₂ ) выходного звена 2 по параметру положения (j₁ , S₁ ) входного звена 1 (j_j – угол поворота, S_j – линейное смещение звена j). Величина i ₁₂ определяется по формулам:

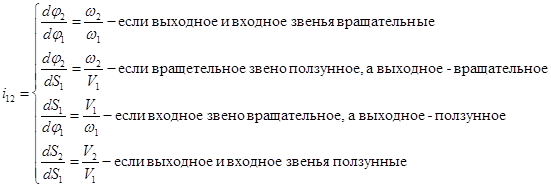
здесь w₁ , w₂ , V₁ , V₂ – угловая и линейная скорость звеньев 1 и 2.

Для механизмов, в которых входные и выходные звенья имеют равномерные движения вместо понятия передаточное отношение i ₁₂ удобнее пользоваться понятием ход S_jk механизма , под которым понимают угловое (или прямолинейное) перемещение ведомого звена 2 за один оборот (или один мм ) перемещения ведущего звена 1. В зависимости от типа передач ход S₁₂ равен:

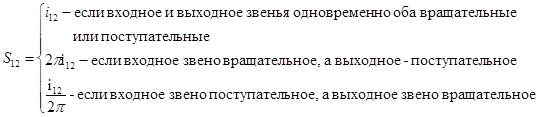
Если механизм сложный (кинематическая цепь механизмов с n подвижными звеньями), то передаточное отношение i _{1 n} от звена 1 к звену n равно:

, (6)

то есть передаточное отношение сложного механизма равно произведению передаточных отношений простых механизмов. Соответственно, если перемещения звеньев в механизме определяется с помощью ходов S_jk простых механизмов, то xод S _{1 n} сложного механизма:

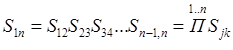(7)

5.2. Равномерность (линейность) механизма. Это свойство определяется постоянством хода или передаточного отношения в механизме. Если, например, j₁ – угол поворота входного звена, j₂ – угол поворота выходного звена и j₂ =i₁₂ j₁ , где i₁₂ =const, то механизм линейный; если i₁₂ ¹const, то механизм неравномерный. Наличие в сложном механизме хотя бы одного простого неравномерного механизма делает весь сложный механизм тоже неравномерным.

В таблице 3 приведены основные типы станочных равномерных механизмов, их ходы S₁₂ и передаточные отношения i₁₂ . В примечании к табл.3 указаны расчетные параметры этих механизмов.

Нелинейность движения механизма оценивают коэффициентом неравномерности равным:

, (7)

где D - диапазон скоростей, D = V_max /V_min ; V_max , V_min – скорость (наибольшая и наименьшая) на выходном звене механизма. У равномерных механизмов . Равномерными являются зубчатые, винтовые, фрикционные и некоторые другие механизмы.

5.3. Реверсивность механизма – свойство изменять направление движения на выходном звене при неизменном направлении движения входного звена. Достигается это либо переключением специально вводимых в сложный механизм реверсивных устройств ([3, стр.74]), либо без переключения, так как это свойство органически присуще данному механизму (например, кривошипному или кулачковому). В переключаемых реверсивных механизмах различают два состояния и соответствующие им два передаточных отношения или хода i_{P 1} , i_{P 2} или S_{P 1} , S_{P 2} , которые обычно одинаковы и постоянны по величине, но отличаются друг от друга знаком. В большинстве шарнирно-рычажных и кулачковых реверсивных механизмах передаточное отношение обычно переменное по знаку и величине.

5.4. Обратимость механизма . Это свойство механизма позволяет передавать движение в обоих направлениях (от звена 1 к звену n и, при необходимости, от звена n к звену 1). Такая особенность механизмов объясняется, в основном, трением в кинематических парах. В необратимых механизмах в результате самоторможения в одной или в нескольких парах движение возможно только в одном направлении. Самотормозящими и, следовательно, необратимыми могут быть винтовые, кулачковые, некоторые зубчатые (например, червячные) и другие передачи скольжения. Напротив, передачи качения являются, как правило несамотормозящими (обратимыми), так как в зацепление между витками (зубцами) звеньев вводят тела качения (шарики или ролики) и коэффициент трения очень мал. Например, в передаче «винт-гайка качения» небольшой нажим (от руки) на гайку вдоль ее оси приводит винт во вращение. Для обратимых механизмов имеет место равенство i_{1 n} =1/i_{n 1} , то есть передаточное отношение (и ход) в механизме от звена 1 к звену n обратно передаточному отношению i_{n 1} (ходу) от звена n к звену 1. Если хотя бы одна кинематическая пара в механизме самотормозящая, то механизм в целом необратимый.

5.5. Регулируемость механизма . Данное свойство определяется возможностью существенного изменения (или небольшой корректировки) какого-либо параметра движения в механизме. Изменяемыми параметрами движения могут быть: длина хода (угловой или линейный путь), скорость (угловая или линейная), направление движения и исходное положение одного из звеньев механизма. Регулировки в механизмах достигаются переключением коробок скоростей и подач, изменением относительного положения или длины одного из звеньев или заменой звеньев (сменных кулачков или шестерен и т.д.), а также введением в механизм специальных корректирующих устройств (см. [3, стр.66,67]).

В общем случае регулируемость механизма по параметру x_j на выходном звене характеризуется диапазоном D_X регулирования, D_X =x_max / x_min , где x_max , x_min – максимальное и минимальное значения регулируемого параметра. В качестве параметра x_j обычно выбирают линейную или угловую скорость, угловую частоту (в оборотах в минуту или в двойных ходах в мин), путь (угловой или линейный) и другие характеристики.

6. ПРИМЕРЫ АНАЛИЗА МЕХАНИЗМОВ

6.1. Кулачково-рычажный механизм привода подачи поперечного суппорта токарного станка-автомата.

1. Механизм преобразует вращение В₁ сменного кулачка 1 (рис.3) в поступательное движение П₇ суппорта 7. Промежуточные звенья:

2-ролик, 3 и 4– коромысла с зубчатыми секторами, 5- шатун,