Реферат: Изучение свободных колебаний и измерение ускорения свободного падения
решение которого известно как:
(15)
Из выражения (15) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w 0 и периодом
(16)
где L=J/(ml) – приведенная длина физического маятника.
Тока О' на продолжении прямой ОС , отстоящая от оси подвеса на расстоянии L , называется центром качаний физического маятника (см. рис.1). Применяя теорему Штейнера, можно показать, что ОО ’ всегда больше ОС= l . Точка подвеса О и центр качаний О ’ обладают свойством взаимозаменяемости : если ось подвеса сделать проходящей через центр качаний О ’ , то точка О прежней оси подвеса станет новым центром качаний. При этом период колебаний физического маятника не изменится, а расстояние между точками подвеса будет равно приведенной длине маятника.
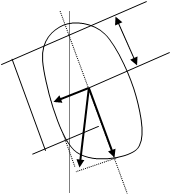
` P=m ` g
Рис. 1
1.3.2. Математический маятник
Математический маятник – идеализированная система, состоящая из материальной точки массой m , подвешенной на невесомой нерастяжимой нити, и колеблющаяся под действием силы тяжести.
Момент инерции математического маятника J =ml, где l - длина маятника. Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся масса физического маятника сосредоточена в одной точке – центре масс, то, подставив выражение момента инерции математического маятника в формулу (16), получим известное выражение для малых колебаний математического маятника.
(17)
Сравнивая формулы (16) и (17) видим, что, если приведенная длина физического маятника равна длине математического маятника, то их периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника – это длина такого математического маятника, период колебаний данного физического маятника.
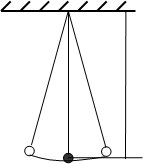 |
l
m
Рис.2
1.3.3 Оборотный маятник
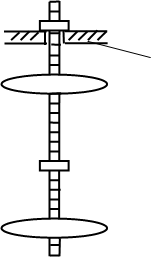
Оборотный маятник является частным случаем физического маятника и состоит из стального стержня 2,двух легких опорных призм 3 и двух массивных грузов 1, имеющих форму чечевиц (рис.3). Призмы и чечевицы могут перемещаться по стержню и фиксироваться с помощью винтов. Если маятник вывести из положения равновесия то он будет совершать колебания в вертикальной плоскости, опираясь нижним ребром одной из призм на закрепленную на массивном штативе опорную площадку 4.
Соотношение T = 2 p J/mgl (см. Формулу (16)) может быть использовано для определения ускорения силы тяжести g. Для этого необходимо измерить период колебания маятника T , расстоние l между осью качания и центром масс, определить момент инерции маятника J относительно оси качания и выразить через них g . Оказывается, однако, что с высокой точностью можно измерить только период колебаний Т маятника, а величины l и J достаточно точно определить не удается. Например, для нахождения расстояния l от оси качаний до центра масс маятника необходимо предварительно определить положение центра масс, что сделать точно довольно трудно.
![]() 3
3
 |
4
1
![]()
![]() 3
3
![]() 1
1
![]()
![]() x
x
![]()
Рис.3
Достоинством метода оборотного маятника для определения ускорения свободного падения является то, что величины J и l не входят в расчетную формулу для g . Перейдем к обсуждению этого метода. Согласно теореме Гюйгенса-Штейнера, момент инерции физического маятника относительно оси качаний О (рис.1)