Реферат: Кинетика двухатомного газа

Займемся вычислением свободной вращательной энергии. Если температура настолько высока, что

(«вращательный квант» ћ²/2I мал по сравнению с T)1 ), то в сумме (3) основную роль играют члены с большими К. Но при больших значениях К вращение молекулы квазиклассично. Поэтому в этом случае статистическая сумма Zвр может быть заменена соответствующим классическим интегралом:

(9)

где ε(М)—классическое выражение кинетической энергии вращения как функции момента вращения М. Вводя связанную с молекулой вращающуюся систему координат ξ, η, ζ, с осью ζ, вдоль оси молекулы и, имея в виду то, что двухатомная молекула обладает двумя вращательными степенями свободы, а момент вращения линейной механической системы перпендикулярен к ее оси, пишем:

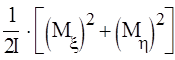ε(M)= (10)

Элемент dτ вр есть деленное на (2лћ)² произведение дифференциалов dM ξ dM η и дифференциалов соответствующих M ξ иM η «обобщенных координат», т. е. бесконечно малых углов поворота вокруг осей

ξ и η: d φξd φη1 ).Но произведение двух бесконечно малых углов поворота вокруг осей ξ и η есть не что иное, как элемент телесного угла d 0 ζ для направления третьей оси ζ; интегрирование по телесному углу даст 4π. Таким образом, имеем 2 ):

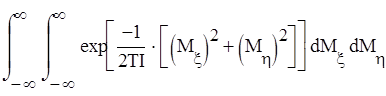Zвр=4π/(2πћ)² =

=2IT/ћ²

Отсюда свободная энергия

Fвр =-NT lnT-NT ln2I/ћ² (10)

Таким образом, при рассматриваемых не слишком низких температурах вращательная часть теплоемкости оказывается постоянной и равной C вр=1 в соответствии с общими результатами классического рассмотрения идеального газа (по ½ на каждую вращательную степень свободы).Вращательная часть химической постоянной равна ξвр=ln(2I/ћ²). Мы увидим ниже, что существует значительная область температур, в которой выполнено условие T>>ћ²/2I и в то же время колебательная часть свободной энергии, а с нею и колебательная часть теплоемкости отсутствуют. В этой области теплоемкость двухатомного газа равна Cν=Cпос+Cвр, т.е.

Cν=5/2, Сp=7/2, (11)

а химическая постоянная ξ= ξпос+ ξвр:

(12)

В обратном предельном случае низких температур

T<<ћ²/2I

достаточно сохранить два первых члена суммы:

Zвр=1+3exp(-ћ²/IT),

и для свободной энергии получим в том же приближении:

Fвр=-3NTexp(-ћ²/IT). (13)

Отсюдаэнтропия

Sвр=3N ћ²/(IT)[exp(-ћ²/IT)](1+ IT/ ћ²) (14)

и теплоемкость

Свр=3N(ћ²/IT) ² exp(-ћ²/IT). (15)

Таким образом, вращательные энтропия и теплоемкость газа при T→0 обращаются в нуль в основном по экспоненциальному закону. При низких температурах,

Следовательно, двухатомный

газ ведет себя как одноатомный; Cвр как его теплоемкость, так и химическая постоянная имеют те же значения, которые имел бы одноатомный газ с части- цами массы m.

В общем случае произвольных 2IT/ ћ²