Реферат: Кинетика двухатомного газа

Некоторые (правда, весьма немногочисленные) молекулы обладают в своем нормальном электронном состоянии отличным от нуля орбитальным моментом или спином.

Существование отличного от нуля орбитального момента Λ приводит, как известно, к двукратному вырождению электронного терма, соответственно двум возможным направлениям этого момента относительно оси молекулы 1 ). Это обстоятельство отразится на термодинамических величинах газа в том отношении, что благодаря удвоению статистической суммы к химической постоянной добавится величина

(33)

Наличие не равного нулю спина S приводит к расщеплению на 2S+1 термов; интервалы этой тонкой структуры, однако, настолько ничтожны (при Λ=0), что при вычислении термодинамических величин ими можно всегда пренебречь. Наличие спина приводит лишь к увеличению кратности вырождения всех уровней в (2S+1) раз, соответственно чему к химической постоянной добавится величина

(34)

Особого рассмотрения требует тонкая структура, возникающая при S≠0, Λ≠0 . Интервалы тонкой структуры при этом могут достигать значений, делающих необходимым их учет при вычислении термодинамических величин. Выведем формулы для случая дублетного электронного терма 2 ).

Каждая компонента электронного дублета имеет свою колебательную и вращательную структуру, параметры которой для обеих компонент можно считать одинаковыми. Поэтому в статистической сумме (2) появится еще один множитель:

где g 0 , g 1 ,—кратности вырождения компонент дублета, Δ—расстояние между ними. К свободной энергии соответственно прибавится «электронная» часть, равная

(35)

Выпишем также «электронную» теплоемкость, которая должна быть добавлена к остальным частям теплоемкости:

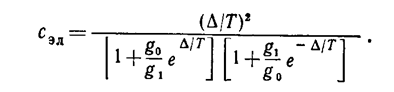(36)

В обоих пределах Т→ 0 и Т→ ∞ Сэл, естественно, обращается в нуль, а при некоторой температуре Т~∆ имеет максимум.

Литература:

1. В. Г. Левич Курс Теоретической Физики .Том 1.

М. Наука. 1969

2. Л. Д. Ландау и Е. М. Лифшищ Статистическая Физика . Том 5. М. Наука. 1964

3. А. В. Митин и О. С. Зуева Введение в квантовую механику. Часть1. М. МЭИ. 1996

1 стр.151, Л.Д.Ландау, Е.М.Лифшиц: “Статистическая физика”.:1964 г.

1 Фактически это условие всегда выполняется для всех газов, за исключением обоих изотопов водорода. Для примера укажем значения ћ²/2kI для некоторых молекул: Н2:85,4°; D2:43°; HD:64°; N2:2,9°; O2:2,1°; Сl2:0,36˚; N0:2,4°; HCI:15,2°.

1 Необходимо иметь в виду, что такой способ написания в известном смысле условлен, так как d φξ и d φηне являются полными дифференциалами какой бы то ни было функции положения осей.

2 Это значение Zврможно получить также и иным способом: считая числа К в сумме (3) большими и заменяя суммирование интегрированием по К, найдем:

Zвр ≈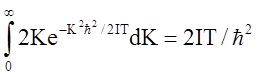

1 Можно получить асимптотическое разложение термодинамических величин при больших значениях 2TI/ ћ². Для теплоемкости первые два члена разложения равны: Свр=1+1/45(ћ²/2TI)². Это разложение дает плохое приближение к функции Свр(T).

1 Для примера укажем значения ћω/k для некоторых двухатомных газов: Н2: 6100°; N2: 3340°; О2: 2230°; NO: 2690°; НСl: 4140°.

1 В соответствии с классическими результатами.

2 Как видно из рис. 2, Скол в действительности приближается к своему предельному значению 1 уже при Т ≈ ћω (так, при T/ћω=1: Скол==0,93). Практическое условие применимости классических выражений можно написать как Т >> ћω/3.

1 Это же значение получается путем замены суммирования по v интегрированием по dv .

1 Строго говоря, происходит расщепление терма на два уровня (так называемое Λ-удвоение), расстояние между которыми, однако, настолько ничтожно, что им можно здесь полностью пренебречь.

2 Такой случай осуществляется у NO; нормальный электронный терм молекулы NO есть дублет П1/2,3/2, с шириной, равной (в градусах) ∆=178°. Обе компоненты дублета двукратно вырождены.