Реферат: Книга S.Gran A Course in Ocean Engineering. Глава Усталость

В некоторых случаях этот момент является достаточным для оценки усталостного ресурса при среднеквадратических значениях напряжений имеющих гамма распределение. Для того, чтобы найти собственно плотность вероятности f(S) , выражение (4.7.5) может быть интегрировано аналитически, но лишь в ограниченном числе случаев. В большинстве случаев, приближенное гамма распределение может быть найдено различными путями. Это подробно описано в главе 4.5, а здесь будет лишь подведен итог.

Функция плотности вероятности для распределения размахов напряжений для больших интервалов времени может быть записана как в (4.5.23):

где параметры d , k и D определены как функции неизвестных параметров a , h , b , j и B . Есть, по крайней мере, три метода для их получения:

1. Элементарный метод, глава 4.5.1;

2. Метод логарифмических моментов, глава 4.5.3;

3. Метод седловой точки (метод перевала), глава 4.5.5.

Элементарный метод, глава 4.5.1, широко использует удобные свойства двухпараметрового распределения Вейбулла (Weibull ). Однако, т.к. это частный случай основного гамма распределения, то можно заранее принять, что все параметры формы распределения равны единице. Это предполагает, что в распределениях вероятностей (4.7.1), (4.7.4) и (4.7.7) будет

Масштабный параметр D в заданном большом интервале времени вычисляют из (4.5.12) и параметр наклона k находят из таблицы 4.5.1. В действительности, масштабный параметр D связанный с предельной амплитудой для большого интервала времени, обозначенной в (4.5.12) через Y_c , часто бывает удобен, т.к. усталостный ресурс и вероятность перегружения описываются во многом одними и теме же переменными.

Метод логарифмических моментов, глава 4.5.3, используют для получения точных значений для первых трех логарифмических моментов для распределения вероятностей (4.7.7). Параметр формы d определяют из (4.5.35). Затем, параметр наклона k вычисляют из (4.5.36), и наконец, масштабный D параметр находят из (4.5.37). Этот метод дает хорошее соответствие в центральной области распределения и, т.о., наиболее пригоден для расчетов на усталость. Метод является наиболее общим, т.к. все параметры формы распределения a , b и d в (4.7.8) могут иметь произвольные значения.

Метод седловой точки, глава 4.5.5, является асимптотическим методом, который дает наилучшие результаты для оценки предельных напряжений. Он может быть удобен для усталостных целей из-за его численной простоты. Здесь параметр формы d задан выражением (4.5.82). Параметр наклона k задан (4.5.86), масштабный параметр D (4.5.87). Подобно элементарному методу, этот метод определяет не только предельные напряжения, но еще и напряженное состояние для короткого интервала времени, при котором появление этого цикла предельных напряжений наиболее вероятно. Это условие определяют с помощью масштаба напряжений X_c , данного в (4.5.92) и продолжительности (4.5.95) измеренной за n циклов. Метод седловой точки требует, чтобы параметр формы для малого отрезка времени a в (4.7.1) был равен единице.

Коэффициент концентрации напряжений. Прежде, размах напряжений S вводился без дальнейшего пояснения. Однако, в усталости элементов конструкции и тем более в механике разрушения, важно рассматривать напряжения на верном структурном уровне, а также верную компоненту тензора напряжений или комбинацию компонент. Для этих целей, вводят коэффициент концентрации напряжений в качестве связи между общими и местными напряжениями.

Например, как упоминалось в главе 3.8.6, эквивалентный брус (корпус судна рассматривается как балка) может быть подвергнут в средней части вертикальному изгибающему моменту M . Этот изгибающий момент вносит общие продольные напряжения s _global в корпусе корабля. Соотношение между ними выражается через модуль сечения корпуса W , определенный в (3.1.18) так, что s _global =M /W . Посмотрите рис. 4.7.2. Теперь предположим, что в корпусе есть прямоугольный люк. Продольные напряжения вдоль поперечного края люка обязательно равны нулю так, что в прилегающей области корпуса вызываются более высокие напряжения, особенно в углах. Предполагается, что местное значение продольных напряжений пропорционально общему напряжению, соотношение задается теоретическим (геометрическим) коэффициентом концентрации напряжений K_t , так, что s _local =K_t s _global .

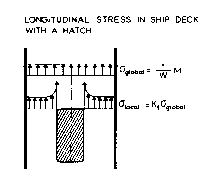
Рис. 4.7.2 Концентрация напряжений, обусловленная наличием люка в корпусе корабля. Общие продольные напряжения, вызванные изгибающим моментом, на которые оказывает влияние люк, порождают концентрацию напряжений в углах.

В некоторых конструкциях, например в соединениях труб, коэффициент концентрации напряжений будет изменяться вблизи замкнутого контура края элемента в достаточно сложном образце, являясь причиной роста вплоть до критических значений, часто называемых “hot spots ” (т.е. области повышенных напряжений). В некоторых данных по усталости, таких как в первом издании работы /6/, элементы конструкции классифицируют согласно показателю влияния надреза (эффективного коэффициента концентрации напряжений) K_f , который используют при построении усталостных кривых. Эффективный коэффициент концентрации напряжений является более определенным коэффициентом концентрации напряжений, преобразованным для того, чтобы учесть конкретную усталостную прочность материала. Для хрупких материалов эффективный коэффициент концентрации напряжений K_f близок к теоретическому коэффициенту K_t . Для пластичных материалов он может быть значительно ниже, отклонение задается индивидуальным коэффициентом чувствительности материала к концентрации напряжений.

Мы будем рассматривать размах напряжений S в описанных выше функциях вероятности как номинальные напряжения. Это может относится к общим, местным и сублокальным напряжениям в зависимости от обстоятельств, в основном к тем типам напряжений, которые необходимы для S-N кривых. Некоторые S-N кривые требуют, чтобы коэффициент концентрации напряжений включал компоненты номинальных напряжений. Другие S-N кривые учитывают возможные коэффициенты концентрации напряжений в соответствующем элементе конструкции.

В механике разрушения тензор номинальных напряжений относится к компонентам сублокальных напряжений, т.к. они появляются в области растрескивания, когда трещин еще нет. Действительное физическое напряженное состояние описывают с помощью переменной интенсивности локальных напряжений, которая связана с номинальными напряжениями геометрической функцией, а она, в свою очередь, зависит от размера трещины. Однако более подробно это будет описано в главе 4.7.5.

Глава 4.7.2 Данные по усталости.

Как уже упоминалось во введении, в принципе, есть два различных метода для предсказания усталостного ресурса, а именно, метод Палмгрена-Майнера и метод механики разрушения. Оба метода полагаются на лабораторные данные, но различных типов. Первый метод основан на S-N кривых, он будет рассмотрен в этой главе. Метод механики разрушения основан на da /dN кривых, он будет кратко затронут в главе 4.7.5.

Общая информация по S-N кривым. S-N кривые показывают число циклов N_f , которое образец может выдержать до разрушения. Все циклы в испытании имеют определенный размах напряжений или амплитуду и измерение на одном образце дает одну точку на кривой. Естественно, общая тенденция такова, что чем меньше размах напряжений S , тем больше ресурс N_f . Кроме того, участки кривых зависят от нескольких физических факторов и могут быть представлены в различных математических формах. Для этого мы можем дать определение двух основных типов:

1. S-N кривые с логарифмическим масштабом на обеих осях (далее – логарифмические кривые), которые являются линейными или кусочно-линейными, при этом logS находится напротив logN .

2. S-N кривые с логарифмическим масштабом на одной из осей (далее – полулогарифмические), которые являются линейными, при этом размах напряжений S на линейной шкале находится напротив logN .

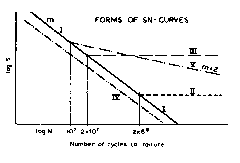
Рис. 4.7.3 Схема изображающая различные S-N кривые,в данном случае для сварных стальных соединений.

Кривые могут содержать, либо не содержать предел усталости (предел выносливости) S₀ , т.е. нижний предел размаха напряжений S , ниже которого ресурс бесконечен. Для сварных стальных соединений чаще всего используют S-N кривые в логарифмической форме. S-N кривые для нержавеющей стали, надрезанных стальных элементов, алюминия, проволочных тросов и т.д. чаще всего представлены в полулогарифмической форме. Примеры логарифмических S-N кривых показаны на рис. 4.7.3. Примеры полулогарифмических кривых есть на рис. 4.7.6.

Сварные стальные соединения. Усталостные трещины в стальных конструкциях часто ограничены сварными соединениями. Опыт показывает, это является причиной того, что усталостные повреждения ограничены этими областями. Данные S-N кривые рекомендованы для расчета сварных стальных соединений имеющих формы показанные в табл. 4.7.3. В дальнейшем мы будем ссылаться на различные формы кривых, как то:

1. S-N кривые без предела усталости, такие как I и IV.

2. S-N кривые с пределом усталости, такие как II и III.

3. Билинейные S-N кривые, такие как V.

Все кривые построены на основе кривой I, которая имеет аналитическую, логарифмическую форму:

Безразмерный параметр m определяет наклон кривой. S₁ – масштабный параметр, который имеет ту же размерность, что и размах напряжений S . Он может быть понят как фиктивный размах напряжений, который определяет усталостные повреждения после одного цикла. Если S представляет вместо размаха напряжений (двойной амплитуды) единичную амплитуду напряжений, то S₁ также должен быть преобразован с амплитуду напряжений (половину размаха). Чаще всего в литературе используют альтернативный параметр A . Однако, это может вызвать затруднения при смене единиц измерения. Для описания ресурса статистически, при данном размахе напряжений, обычно принимают, что A является нормальным логарифмом так, что logA нормален при данном среднем значении и среднеквадратическом отклонении. Номинальное значение A обычно дано как 95.5% выживаемости, как показано в табл. 4.7.2. Стандартные значения, закрепленные за параметрами m и S₁ (или logA ), обычно определяют ряд классов усталости: B, C, D, E, F, F₂ , G, W, T и X.