Реферат: Кольца. Примеры колец. Гомоморфизмы и изоморфизмы колец. Подкольца. Кольцо целых чисел
II. Множество 
- замкнуто относительно операций 
и алгебраическая система 
является системой натуральных чисел (системой Пеано).
Для 
, 
Для 
, 
Для , 
Для , 
Для , 
Для , 
Аксиома индукции: пусть 
. Если множество удовлетворяет условиям:
а) 
б) , 
, то 
III. Аксиома минимальности.
Если 
и обладает свойствами:
а) 
б) 
, то 
.
Свойства целых чисел.
Теорема 1. О делении с остатком.
| 
, где 
. Число 
называется делимым, 
- делителем, 
- частным, 
- остатком при делении на .
Доказательство. Докажем существование хотя бы одной пары чисел , . Для этого рассмотрим множество 
. Множество 
содержит как отрицательные, так и неотрицательные числа, пусть - наименьшее неотрицательное число в , тогда 
. Докажем, что 
, предположим противное 
. Рассмотрим число 
. 
противоречие с выбором . Доказано, что 
, . Докажем единственность чисел и , пусть . 
, 
. Докажем, что 
, предположим противное 
. Пусть 
. Имеем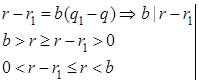 
противоречие, так как между числами 
нет чисел, делящихся на . Доказано, что , если , то 
, а отсюда следует, что 
. Доказана единственность чисел и .
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001