где Ω область определения Ψ(x,y,z).

Ψ(x,y,z) волновая функция прямого физического смысла не имеет. Смысл имеет квадрат модуля волновой функции |Ψ|2 как плотность вероятности обнаружения частицы в точке пространства (x,y,z) области определения Ψ(x,y,z).

Вывод алгоритма

В работе был создан алгоритм для вычисления этой плотности. Искалось решение в виде: и выведены следующие формулы:

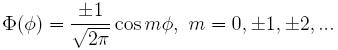
Для решения уравнения Θ(θ) необходимо разбираться в следующих понятиях.

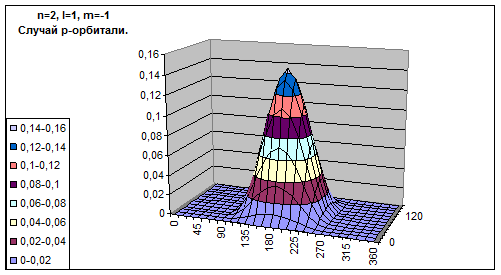
Орбиталь – это некоторый объем пространства, где вероятность нахождения электрона составляет не менее 90%.

Квантовые числа - энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

1. Главное квантовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n=1,2,3,...).

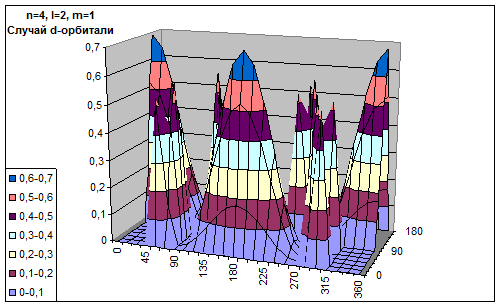
2. Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1 (l = 0,1, 2, 3, ..., n-1 ). Каждому значению l соответствует орбиталь особой формы: l=0 – s-орбитали; l=1 – р-орбитали (3 типа, отличающихся магнитным квантовым числом m ); l=2 – d-орбитали (5 типов), l=3 – f-орбитали (7 типов).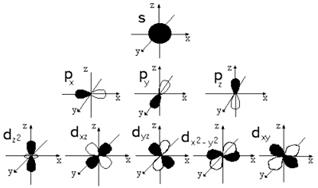

3. Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от – l до + l , включая 0. Например, при l=1 число m принимает 3 значения: +1, 0, -1 , поэтому сущ. 3 типа: p _x ,p _y ,p _z .

4. Спиновое квантовое число s может принимать лишь два возможных значения ±½. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемого спином. Для обозначения электронов с различными спинами используются символы: ↑ и ↓.

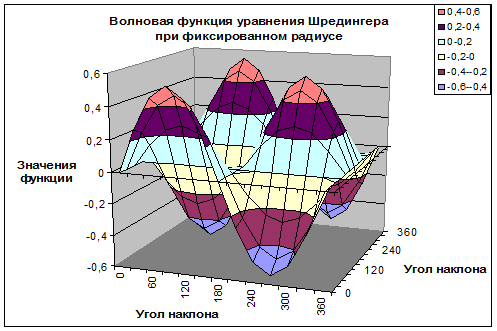
Произведение найденных функций Θ(θ) и Ф(ф) представляет собой угловую часть волновой функции и называется сферической гармоникой Y _lm (θ,φ)

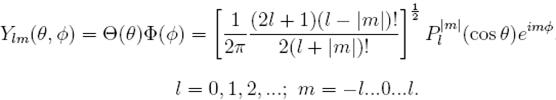
Решение радиального уравнения было следующим:

Полученные результаты

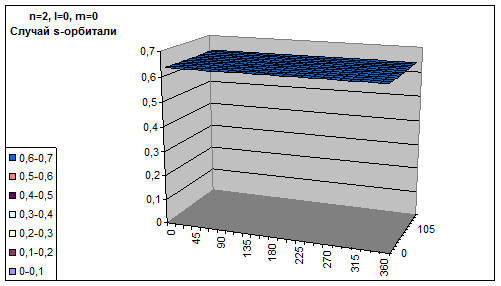
На основе выведенной формулы была составлена программа для подсчета вероятности нахождения электрона в точке пространства при конкретных квантовых числах. Графики вероятностей обнаружения частицы в данных углах при максимально вероятном при этих углах радиусе выглядят так.

Литературный обзор

Основоположником отечественн