Реферат: Конечные разности. Погрешности
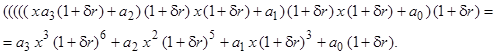
Учитывая, что ![]() , последнее выражение дает возможность после раскрытия скобок выделить из суммы и оценить сначала абсолютную погрешность, а по абсолютной погрешности – относительную:
, последнее выражение дает возможность после раскрытия скобок выделить из суммы и оценить сначала абсолютную погрешность, а по абсолютной погрешности – относительную:
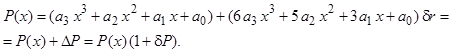
Условные арифметические операторы с проверкой равенства операндов необходимо заменять проверкой вида: ![]() .
.
2. Конечные разности
2.1 Определение конечных разностей
Конечная разность «вперед» для таблично заданной функции в i -той точке определяется выражением: ![]() , где функция
, где функция ![]() задана, как функция целочисленного аргумента с единичным шагом по аргументу i .
задана, как функция целочисленного аргумента с единичным шагом по аргументу i .
Для аналитически заданной и протабулированной с постоянным шагом h функции ![]() определяющее соотношение имеет вид:
определяющее соотношение имеет вид:
![]() .
.
Преобразование таблицы функции ![]() в функцию целочисленного аргумента
в функцию целочисленного аргумента ![]() осуществляют при помощи линейного соотношения между аргументами x и i :
осуществляют при помощи линейного соотношения между аргументами x и i : ![]() .
.
Коэффициенты a и b находят из системы уравнений, получаемой в результате подстановки в пределах заданной таблицы вместо x и i сначала начальных значений аргументов ![]() , а затем конечных
, а затем конечных ![]() . При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом
. При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом![]() (
(![]() ). Тогда для таблицы с (n+ 1) – й строками:
). Тогда для таблицы с (n+ 1) – й строками:
![]() ,
,
![]()
Повторные конечные разности n -го порядка в i -той точке для табличной функции ![]() определяются соотношением
определяются соотношением
![]() .
.
2.2 Конечно-разностные операторы
Линейность конечно-разностного оператора ![]() позволяет ввести конечно-разностный оператор сдвига
позволяет ввести конечно-разностный оператор сдвига ![]() и многочлены от оператора
и многочлены от оператора ![]() с целыми коэффициентами, такие, как
с целыми коэффициентами, такие, как ![]() , где
, где ![]() должно рассматриваться как оператор повторной разности k -того порядка.
должно рассматриваться как оператор повторной разности k -того порядка.
Действие любого многочлена ![]() на функцию g (i ) определяется как
на функцию g (i ) определяется как
![]() .
.
Применение оператора сдвига к g (i ) преобразует последнее в g (i +1):
g (i +1) = E g (i ) = (1+![]() ) g (i )= g (i ) +
) g (i )= g (i ) + ![]() g (i ).
g (i ).
Повторное применение оператора сдвига позволяет выразить (i+n ) – е значение ординаты функции g через конечные разности различных порядков:
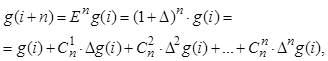
где ![]() – число сочетаний из n элементов по k ;
– число сочетаний из n элементов по k ;
![]() – многочлен степени k от целой переменной n (
– многочлен степени k от целой переменной n (![]() ), имеющий k сомножителей. При k=n
), имеющий k сомножителей. При k=n ![]() .
.
В силу линейности оператора сдвига можно конечно-разностный оператор выразить, как ![]() , и определить повторные конечные разности через многочлены от операторов сдвига так
, и определить повторные конечные разности через многочлены от операторов сдвига так ![]() .
.
Последнее позволяет формульно выражать n -ную повторную разность через (n +1) ординату табличной функции, начиная с i -той строки: