Реферат: Концепция риска инвестиционного проекта

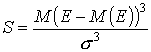. (13)

Экономический смысл коэффициента асимметрии в данном контексте заключается в следующем. Если коэффициент имеет положительное значение (положительный скос), то самые высокие доходы (правый «хвост») считаются более вероятными, чем низкие и наоборот.

Коэффициент асимметрии может также использоваться для приблизительной проверки гипотезы о нормальном распределении случайной величины. Его значение в этом случае должно быть равно 0.

В ряде случаев смещенное вправо распределение можно свети к нормальному прибавлением 1 к ожидаемой величине доходности и последующим вычислением натурального логарифма полученного значения. Такое распределение называют логнормальным. Оно используется в финансовом анализе наряду с нормальным.

Некоторые симметричные распределения могут характеризоваться четвертым нормированным центральным моментом – эксцессом (е):

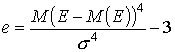. (14)

Если значение эксцесса больше 0, кривая распределения более остроконечна, чем нормальная кривая и наоборот.

Экономический смысл эксцесса заключается в следующем. Если две операции имеют симметричные распределения доходов и одинаковые средние, менее рискованной считается инвестиция с большим эксцессом.

Для нормального распределения эксцесс равен 0.

Выбор распределения случайной величины

Нормальное распределение используют, когда невозможно точно определить вероятность того, что непрерывная случайная величина принимает какое-то конкретное значение. Нормальное распределение предполагает, что варианты прогнозируемого параметра тяготеют к среднему значению. Значения параметра существенно отличающиеся от среднего, т.е. находящиеся в “хвостах” распределения, имеют малую вероятность осуществления. Такова природа нормального распределения.

Треугольное распределение представляет собой суррогат нормального и предполагает линейно нарастающее по мере приближения к моде распределение.

Трапециевидное распределение предполагает наличие интервала значений с наибольшей вероятностью реализации (НВР) в пределах РВД.

Равномерное распределение выбирается, когда предполагается, что все варианты прогнозируемого показателя имеют одинаковую вероятность реализации

Однако, когда случайная величина дискретна, а не непрерывна, применяют биномиальное распределение и распределение Пуассона.

Иллюстрацией биномиального распределения служит пример с подбрасыванием игральной кости. При этом экспериментатора интересуют вероятности “успеха” (выпадения грани с определенным числом, например, с “шестеркой”) и “неудачи” (выпадение грани с любым другим числом).

Распределение Пуассона применяется, когда выполняются следующие условия:

1.Каждый малый интервал времени может рассматриваться как опыт, результатом которого является одно из двух: либо “успех”, либо его отсутствие – “неудача”. Интервалы столь малы, что может быть только один “успех” в одном интервале, вероятность которого мала и неизменна.

2.Число “успехов” в одном большом интервале не зависит от их числа в другом, т.е. “успехи” беспорядочно разбросаны по временным промежуткам.

3.Среднее число “успехов” постоянно на протяжении всего времени.

Обычно распределение Пуассона иллюстрируют примером регистрации количества дорожных происшествий за неделю на определенном участке дороги.

При определенных условиях распределение Пуассона может быть использовано как аппроксимация биномиального распределения, что особенно удобно когда применение биномиального распределения требует сложных, трудоемких расчетов, отнимающих много времени. Аппроксимация гарантирует приемлемые результаты при выполнении следующих условий:

1.Количество опытов велико, предпочтительно более 30-ти (n=3).

2.Вероятность “успеха” в каждом опыте мала, предпочтительно менее 0.1.(p=0.1) Если вероятность “успеха” велика, то для замены может быть использовано нормальное распределение.

3.Предполагаемое количество “успехов” меньше 5 (np=5).

В случаях, когда биномиальное распределение весьма трудоемко, его также можно аппроксимировать нормальным распределением с “поправкой на непрерывность”, т.е. делая допущение, что, например, значение дискретной случайной величины 2 является значением непрерывной случайной величины на промежутке от 1.5 до 2.5.

Оптимальная аппроксимация достигается при выполнении следующих условий: n=30; np=5, а вероятность “успеха” p=0.1 (оптимальное значение р=0.5)

Цена риска

Следует отметить, что в литературе [3,14] и практике помимо статистических критериев используются и другие показатели измерения риска: величина упущенной выгоды, недополученный доход и другие, рассчитываемые, как правило, в денежных единицах. Безусловно, такие показатели имеют право на существование, более того, они зачастую проще и понятнее чем статистические критерии, однако для адекватного описания риска они должны учитывать и его вероятностную характеристику.

На основе проведённого анализа автор предлагает обобщённый комплексный критерий - «цена риска» (C _risk ), который характеризует величину условных потерь возможных при реализации инвестиционного решения: