Реферат: Корпускулярно-хвильовий дуалізм речовини

Розглянемо дифракцію електронів на одній щілині. Нехай пучок електронів із швидкістю  летить в напрямі осіOY так, як це показано на рис. 1.4.

Екран АВ із щілиною шириною d розміщено перпендикулярно до пучка. На другому екраніСД одержано розподіл інтенсивності, який збігається з розподілом інтенсивності при дифракції світла від однієї щілини.

На рис. 1.4 цей розподіл зображено пунктирною лінією. Максимум нульового порядку одержано з кутом дифракції  , який задовольняє умову:

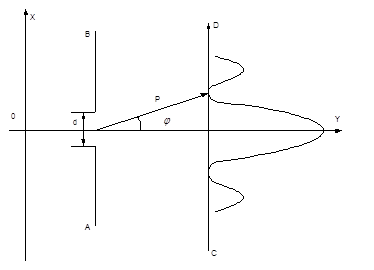
Рис. 1.4

, (1.1.12)

де  ― довжина хвилі, яка відповідає пучку електронів.

З рис. 1.4 видно, що переважна більшість електронів формують нульовий максимум, тому вторинними максимумами в цьому випадку можна знехтувати. Якщо уявити електрони у вигляді механічних частинок, то можна стверджувати, що при їх русі із швидкістю  у напрямі осі OX їх положення визначається з точністю до ширини щілини, тобто

(1.1.13)

В той же час, унаслідок дифракції змінюється напрям швидкості частинок. Враховуючи лише ті електрони, які формують центральний максимум дифракції, похибку у визначенні проекції імпульсу на напрям осі OX знайдемо із умови

. (1.1.14)

З урахуванням (1.1.12) і (1.1.13) одержимо

.(1.1.15)

А оскільки не всі електрони формують центральний максимум, тому

, (1.1.16)

де x іp_x ― похибки у визначені координати й імпульсу частинки; – стала Планка поділена на 2.

Співвідношення (1.1.16) можна узагальнити для всіх напрямків, тому:

,

, (1.1.17)

.

Це і є співвідношення невизначеностей Гейзенберга.

Оскільки точні значення координати й імпульсу для мікрочастинки не існують, то про траєкторію частинки в мікросвіті можна говорити лише з певним наближенням. З цієї точки зору електрони в атомі не мають точних значень електронних орбіт.

У квантовій теорії використовується також співвідношення невизначеностей для енергії Е і часуt , тобто невизначеності цих параметрів задовольняють умову:

, (1.1.18)

де  E ― похибка у визначенні енергії частинки;t ― похибка у визна-ченні часу, коли частинка має енергію E .

Cпіввідношення невизначеностей неодноразово були предметом філософських дискусій. Однак вони не виражають собою певних обмежень пізнання мікросвіту, а лише указують межі використання у таких випадках понять класичної механіки.

Ще раз підкреслимо, що співвідношення невизначеностей не пов'язано з недосконалістю вимірювальної техніки, а є об'єктивною властивістю матерії: таких станів мікрочастинок, у яких і координата, і імпульс частинки мають визначене значення, просто не існує в природі.

Співвідношення невизначеностей допомагають зрозуміти багато особливостей поведінки мікрочастинок і дозволяють швидко й просто оцінити параметри їх стану. Для прикладу розглянемо застосування співвідношень невизначеностей до опису руху електрона в атомі водню.

Будемо вважати, що електрон локалізований в області простору, розміри якого дорівнюють розмірам атома. Тоді невизначеність координати електрона можна прийняти рівною радіусу атома: ∆ x = r . Звідси, відповідно до рівнянь (1.1.17), невизначеність значення імпульсу електрона ∆p =h / (2 r) . Очевидно, що значення самого імпульсу не може бути меншим його невизначеності, тому мінімально можливе значення імпульсу електрона дорівнює

(1.1.19)

Рівняння (1.1.19) можна записати у вигляді p ∆ r = h/2π , або mvr = ћ . Цей результат – не що інше, як умова стаціонарної орбіти електрона в атомі водню відповідно до постулатів Н. Бора . Але, якщо Н. Бор увів свої постулати довільно, і тільки для атома водню, то ми одержали цю умову із загального універсального принципу – співвідношення невизначеностей.