Реферат: Корреляционный анализ
Математически доказано, что условие ![]() соблюдается, если в качестве такого множителя принять значение факторного признака, т.е. если уравнение прямой умножить на х. Кроме рассмотренных функций связи в экономическом анализе часто применяются степенная, показательная и гиперболическая функции. Степенная функция имеет вид Y=axb .
соблюдается, если в качестве такого множителя принять значение факторного признака, т.е. если уравнение прямой умножить на х. Кроме рассмотренных функций связи в экономическом анализе часто применяются степенная, показательная и гиперболическая функции. Степенная функция имеет вид Y=axb .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1 %. При х = 1 a = Y.
Для определения параметров степенной функции вначале ее приводят к линейному виду путем логарифмирования: lg y=lg a+ blg x, а затем строят систему нормальных уравнений:
![]()
Решив систему двух нормальных уравнений, находят логарифмы параметров логарифмической функции a и b, а затем и сами параметры a и b. При помощи степенной функции определяют, например, зависимость между фондом заработной платы и выпуском продукции, затратами труда и выпуском продукции и т.д.
Если факторный признака x растет в арифметической прогрессии, а результативный у - в геометрической, то такая зависимость выражается показательной функцией Y=a+bx . Для определения параметров показательной функции ее также вначале приводят к линейному виду путем логарифмирования: lg y=lg a+ xlg b, а затем строят систему нормальных уравнений:
![]()
Вычислив соответствующие данные и решив систему двух нормальных уравнений, находят параметры показательной функции a и b.
В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы:
Y=a+b/x.
И здесь задача заключается в нахождении параметров a и b при помощи системы двух нормальных уравнений:
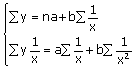
При помощи гиперболической функции изучают, например, связь между выпуском продукции и себестоимостью, уровнем издержек обращения (в процентах к товарооборот и товарооборотом в торговле, сроками уборки и урожайностью и т.д.).
Таким образом, применение различных функций в качестве уравнения связи сводится к определению параметров уравнения по способу наименьших квадратов при помощи системы нормальных уравнений.
В малых совокупностях значение коэффициента регрессии подвержено случайным колебаниям. Поэтому возникает необходимость в определении достоверности коэффициента регрессии. Достоверность коэффициента регрессии определяется так же, как и в выборочном наблюдении, т.е. устанавливаются средняя и предельная ошибки для выборочной средней и доли.
Средняя ошибка коэффициента регрессии определяется по формуле:
![]()
где σ2 0 - случайная дисперсия;
σ2 - общая дисперсия,
n - число коррелируемых пар.
4 Измерение тесноты связи
Чтобы измерить тесноту прямолинейной связи между двумя признаками, пользуются парным коэффициентом корреляции, который обозначается r.
Так как при корреляционной связи имеют дело не с приращением функции в связи с изменением аргумента, а с сопряженной вариацией результативных и факторных признаков, то определение тесноты связи, по существу, сводится к изучению этой сопряженности, т.е. того, в какой мере отклонение от среднего уровня одного признака сопряжено с отклонением другого. Это значит, что при наличии полной прямой связи все значения (х-X) и (у-Y) должны иметь одинаковые знаки, при полной обратной - разные, при частичной связи знаки в преобладающем числе случаев будут совпадать, а при отсутствии связи - совпадать примерно в равном числе случаев.
Для оценки существенности коэффициента корреляции пользуются специально разработанной таблицей критических значений r.
Коэффициент корреляции r применяется только в тех случаях, когда между явлениями существует прямолинейная связь. Если же связь криволинейная, то пользуются индексом корреляции, который рассчитывается по формуле:
![]()
где у - первоначальные значения;
![]() - среднее значение;
- среднее значение;
Y - теоретические (выровненные) значения переменной величины.