Реферат: Корреляционный анализ

- тесноту связи;

- влияние отдельных факторов на общий результат.

Определение формы связи.

Определение формы связи сводится обычно к отысканию уравнения связно с факторами x,z,w,...v. Так, линейное уравнение зависимости результативного признака от двух факторных определяется по формуле

=a₀ +a₁ x+a₂ z

Для определения параметров а₀ , a₁ и а₂ , по способу наименьших квадратов необходимо решить следующую систему трех нормальных уравнений:

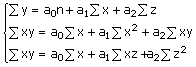
Измерение тесноты связи.

При определении тесноты связи для множественной зависимости пользуются коэффициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреляции. Так, при изучении связи между результативным признаком y и двумя факторными признаками - х и z, нужно предварительно определить тесноту связи между у и х, между у и z, т.е. вычислить коэффициенты парной корреляции, а затем для определения тесноты связи результативного признака от двух факторных исчислить коэффициент множественной корреляции по следующей формуле:

где r_xy , r_zy , r_zx - парные коэффициенты корреляции.

Коэффициент множественной корреляции колеблется в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный результат.

Если коэффициент множественной корреляции возвести в квадрат, то получим совокупный коэффициент детерминации, который характеризует долю вариации результативного признака у под воздействием всех изучаемых факторных признаков.

Совокупный коэффициент детерминации, как и при парной корреляции, можно исчислить по следующей формуле:

R² =σ² _y /σ² _y

где σ² _Y - дисперсия факторных признаков,

σ² _y - дисперсия результативного признака.

Однако вычисление теоретических значений Y при множественной корреляции и сложно, и громоздко. Поэтому факторную дисперсию σ² _Y исчисляют по следующей формуле:

Проверка существенности связи при множественной корреляции по сути ничем не отличается от проверки при парной корреляции.

Поскольку факторные признаки действуют не изолированно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между х и у при постоянном z рассчитывается по следующей формуле:

В настоящее время на практике широкое распространение получил многофакторный корреляционный анализ;

6 Методы измерения тесноты связи

Измерение тесноты связи при помощи дисперсионного и корреляционного анализа связано с определенными сложностями и требует громоздких вычислений. Для ориентировочной оценки тесноты связи пользуются приближенными показателями, не требующими сложных, трудоемких расчетов. К ним относятся: коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов, коэффициент ассоциации и коэффициент взаимной сопряженности.

Коэффициент корреляции знаков основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков, а не на сопоставлении попарно размеров отклонений индивидуальных значений факторного и результативного признаков от средней

(x- ) и (y- ):

i=(u-v)/(u+v),

где u - число пар с одинаковыми знаками отклонений х и у от и ;