Реферат: Кремний, полученный с использованием геттерирования расплава
Величина -g, характеризующая поля центра, является комбинацией упругих постоянных среды и включения, а такжеразмера включения .
При проведении расчетов по формулам (2)—(5) температура, параметры g иW1 варьировали сь с целью изучения их влияния на процесс геттерирования. Результаты численного моделирования представлены на ри с. 1 и 2. Показаны распределения концентрации диполей и поляризации вблизи преципитата радиуса rp для двух случаев, отличающихся знаком упругого поля преципитата. Анализ полученных данных позволяет установить, что независимо от знака упругого поля преципитат а имеет место обогащение диполями пространства вблизи преципитата.
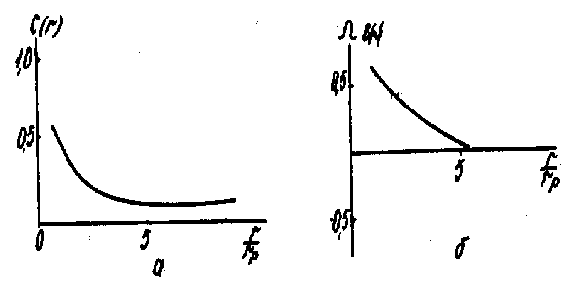
Рис. 1. Распределение диполей (а) и их поляризаци и (б) вблизи сферического преципи тата с отрицательным объемным несоответствием —0.005 .
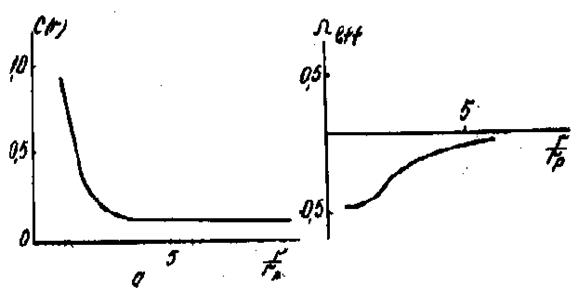
Рис. 2. Распределение дипол ей (6) и их поляризация (б)в близи сфериче ского преци пи тата с положительным объ емн ым несоотве тствием -0.005 .
Диффуз ионная модель процесса ВГ .
Для рассмотрения кинети ки образования рав новесного распределения примеси вокруг преципитата запишем. уравнение диффузии в виде
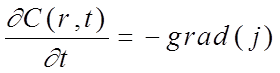
- где j вектор плотности потока частиц определяется выражением
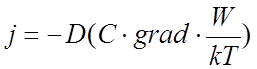
После подстановки и перехода к сферическим координатам уравнение (9) принимает вид:
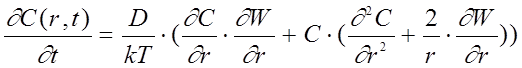
Уравнение (6) совместно с (3) и с соответствующими начальными и граничными условиями описывает эволюцию поля концентраций примесных комплексов С( r ), а приt ® ¥ — равновесное состояние. В случае ограниченного числа частиц граничными условиями являются: на внешней поверхности j=0, на внутренней границе раздела Si—Si02,j= V sC, гдеVs — коэффициент поверхностного массопереноса грани цы раздела кремни й—окисел . Переходя в уравнении (6) к безразмернымпеременным :
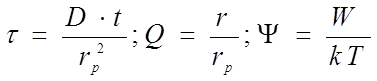
получим :
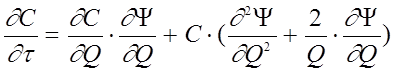 (7)
(7)
Результаты численного решения уравнения (7) показали, что при больших временах равновесное распределение является предельным для кинетических распределений. Для количественного представления эффективности процесса ВГ на рис. 3 представлена величина h -доля примеси, геттерированной на преципитате, как функция безраз мерного времени. Кривые 1 и 2 описывают эффективность процесса ВГ соответственно с учетом и без учета упругого взаимодействия. Параметр g соответствует здесь относительному линейному несоответствию включения и полости в матрице, в которую он вставлен, равному 0,005, что типично для кислородного преципитата в кремнии, выращенном по методу Чохральского. Из рисунка видно, что дополнительный вклад геттерирования, вследствие упругого взаимодействия сопоставим с величиной геттерирования в отсутствие упругого взаимодействия. При этом процесс ВГ при упругом взаимодействии протекает быстрее .
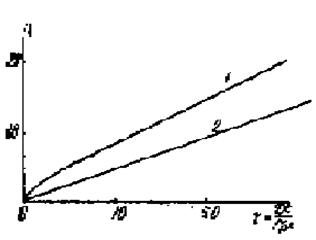 Рис. 3. Дол я геттерированных примесных атомов как функция времени в процентах к их полному числу при начальной кон центрации (С о=10^-8 ): 1 - с уче том вз аимодей ствия примесный комплекс-геттер.
Рис. 3. Дол я геттерированных примесных атомов как функция времени в процентах к их полному числу при начальной кон центрации (С о=10^-8 ): 1 - с уче том вз аимодей ствия примесный комплекс-геттер.
2 - без учета взаи модействия
Развитая модель формирования атмосфер и геттерирования примесных атомов дипольного типа вблизи сферического преципитата показывает, что в условиях формирования комплексов примесный атом — точечный дефект кислородные преципитаты могут служить центрами конденсации примесных атомов. Если на поверхности преципитата происходит распад комплекса, при котором на ней осаждается атом примеси, то для поддержания равновесного значения концентрации потребуется диффузионно-дрейфовый подвод новых комплексов. Таким образом, в условиях- образования подвижных комплексов примесный атом—точечный дефект вдали от преципитата и их распада вблизи его развитая модель дает объяснение механизма геттерирования, который не имеет ограничения по пересыщению и служит «дрейфовым насосом», обеспечивающим уменьшение концентрации примеси в объеме кристалла.
Анализ результатов расчетов позволяет выделить следующие моменты, определяющие свойства процессов ВГ.
-эффективность геттерирования является функцией температуры, причем существует оптимальная температура для максимальной эффективности этого механизма гет терирования;
-геттер (преципитатSiO 2) действует не только как сток для примесей, но и как источник междоузлий Si, которые активируют процесс ВГ;
-собственные междоузлия кремния, инжектируемые растущим преципитатом в объем кристалла, взаимодействуют с геттерируемыми атомам и, и напряжения влияют на увеличение дрейфового потока.