Реферат: Криптосистеми

.

Кожний первісний елемент породжує поле:

.

Криптоперетворення пов’язані з побудуванням пари ключів. Нехай є два користувачі А та В.

А	В
ХА	ХВ

де Х_А , Х_В – випадкові ключі довжиною l_k ;

Y_А , Y_В – відкриті ключі.

При побудуванні використовуються властивості поля.

,

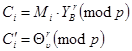де r – сеансовий ключ.

Користувач А передає користувачу В пару . Потім користувач В обчислює:

.

Таким чином, перетворення в полі є зворотнім та однозначним.

Модель криптоаналітика заключається в тому, що необхідно знайти Х_В . Реалізуючи рівняння відносно Х_В одержимо секретний ключ. Стійкість проти атак в полі визначається складністю розв’язання рівняння .

Сутність асиметричних криптоперетворень в групі точок еліптичних кривих

За 20 років розроблено нові математичні апарати, які дозволяють ефективно розв’язувати рівняння, що реалізовані в полях та кільцях. В 90-х роках було запропоновано використовувати криптоперетворення, що базуються на перетвореннях в групі точок еліптичних кривих над полями GF(p), GF(2^m ), GF(p^m ).

Для випадку простого поля:

елементом перетворення є точка на еліптичній кривій, тобто ,що обчислюється за модулем р. Формується ключова пара:

, де .

,

де G – базова точка на еліптичній кривій порядку

Q_A – відкритий ключ, точка на еліптичній кривій з координатами (х_а , у_а ).

Задача криптоаналітика знайти таємний ключ d_A . Складність розв’язку цього рівняння набагато вище, ніж в полі. В полі – субекспоненційна складність, а в групі точок еліптичних кривих – експоненційна складність.

3. СИМЕТРИЧНІ КРИПТОПЕРЕТВОРЕННЯ

Застосовувані на практиці криптоперетворення розділяють на 2 класи по стійкості:

1. обчислювально стійкі.

2. ймовірно стійкі (доказово стійкі).

Основним показником, по якому оцінюються такого роду системи є безпечний час: