Реферат: Критический объем и плотность веществ их прогнозирование
Таким образом, развитие методов прогнозирования потребует, вероятно, и уточнения требований к критериям подобия.
6. ПРОГНОЗИРОВАНИЕ плотности газа и жидкости [6, 17-18]
Перед тем как перейти к прогнозированию, следует напомнить, что в зависимости от принятых температуры и давления вещество может находиться либо в насыщенном, либо в ненасыщенном состоянии. Давление над насыщенной жидкостью равно давлению ее насыщенного пара при данной температуре . Давление над ненасыщенной, переохлажденной или сжатой жидкостью больше давления ее насыщенного пара при избранной для расчета температуре. Для каждой из названных областей P-V-T пространства существуют самостоятельные подходы к прогнозированию плотности.
Прогнозирование плотности индивидуальных веществ с использованием коэффициента сжимаемости
Пример 6.1
Для изобутилбензола, имеющего критическую температуру 650 К, критическое давление 31 атм и ацентрический фактор 0,378, рассчитать с использованием таблиц Ли-Кеслера (табл. 4.6, 4.7):
· коэффициент сжимаемости при 500, 657 и 1170 К и давлении 1-300 атм,
· плотность при 500, 657 и 1170 К и давлении 1-300 атм;
дать графические зависимости:
· коэффициента сжимаемости от давления при указанных температурах,
· плотности от давления при указанных температурах.
Решение
Используем разложение Питцера (уравн. 4.34) и табл. 4.6, 4.7 для коэффициента сжимаемости.
1. Вычислим значения приведенных температур:
![]() = 500/600 =0,769;
= 500/600 =0,769; ![]() = 657/650 =1,01;
= 657/650 =1,01; ![]() = 1170/650 =1,80.
= 1170/650 =1,80.
2. Вычислим значения приведенных давлений:
![]() = 1/31 =0,03226;
= 1/31 =0,03226; ![]() = 300/31 =9,677.
= 300/31 =9,677.
Поскольку диапазон интересующих приведенных давлений совпадает с диапазоном ![]() , рассмотренных Ли-Кеслером, используем информацию о
, рассмотренных Ли-Кеслером, используем информацию о ![]() и
и ![]() для дискретных значений
для дискретных значений ![]() , представленных в табл. 4.6, 4.7.
, представленных в табл. 4.6, 4.7.
Каждое из значений ![]() и
и ![]() получено линейной интерполяцией по температуре. Так, при 500 К (
получено линейной интерполяцией по температуре. Так, при 500 К (![]() = 0,769) и
= 0,769) и ![]() = 0,010 для
= 0,010 для ![]() имеем
имеем
(0,9935-0,9922)/(0,80-0,75)·(0,769-0,75)+0,9922 = 0,9927.
Прогнозирование плотности насыщенных жидкости и пара с использованием уравнений состояния вещества
Нахождение условий насыщения из уравнений состояния представляет собой достаточно сложную задачу, решение которой зачастую невозможно без привлечения вычислительной техники и специального программного обеспечения. Для простых уравнений состояния, таких как уравнение Ван-дер-Ваальса, эта задача может быть решена путем несложных вычислений. Однако необходимо помнить, что на практике при помощи уравнения Ван-дер-Ваальса можно лишь качественно оценить состояние насыщения. Для более точного представления насыщения разработаны другие уравнения состояния и специальные методы.
В данном пособии на примере уравнения Ван-дер-Ваальса рассмотрен подход к нахождению давления насыщения и объемов насыщения жидкости и пара (точки, принадлежащие бинодали), а также условий, определяющих метастабильные состояния вещества (точки экстремумов изотермы).
Пример 6.3
Для изобутилбензола при температурах 400, 500, 600 и 640 К, используя уравнение Ван-дер-Ваальса, рассчитать давление пара и объемы насыщения жидкости и пара. Определить также области метастабильных состояний пара и жидкости при указанных температурах. Критическая температура равна 650 К, критическое давление - 31 атм.
Решение
1. Запишем принцип Максвелла:
Площадь = ![]() .(6.1)
.(6.1)
Выразим из уравнения Ван-дер-Ваальса значение давления и подставим его в подинтегральное выражение. Получим
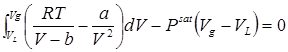 . (6.2)
. (6.2)