Реферат: Критический объем и плотность веществ их прогнозирование

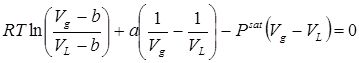.(6.3)

Теперь задача сводится к отысканию значения P sat , при котором выражение 6.3 обратится в тождество. При его нахождении нам потребуется неоднократно определять значения объемов жидкости и пара для заданного P, т.е. находить решения (корни) кубического уравнения.

2. Перепишем уравнение Ван-дер-Ваальса в виде полинома по объему

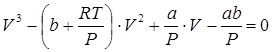.(6.4)

Корни данного уравнения можно найти, воспользовавшись формулами Кардано. Для этого перейдем к приведенному виду кубического уравнения, выполнив следующие преобразования. Обозначим коэффициенты в уравнении (6.4) через

; ;

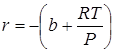и сделаем замену неизвестного V на Y:

;

тогда уравнение (6.4) примет приведенный вид

,(6.5)

где ; .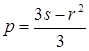

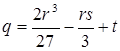Число действительных решений кубического уравнения зависит от знака дискриминанта

.(6.6)

Если D > 0, то уравнение имеет одно действительное решение; если D < 0, то - три действительных решения; и если D = 0, то уравнение имеет либо два действительных решения, одно из которых двукратное, либо одно действительное трехкратное решение (последнее в случае p = q = 0).

В данном примере рассматривается область P-V-T пространства, где сосуществуют пар и жидкость. Для этой области уравнение Ван-дер-Ваальса имеет три действительных решения (дискриминант уравнения (6.5) меньше нуля). При использовании формул Кардано в оригинальном виде корни уравнения выражаются через комплексные величины. Избежать этого можно, если ввести следующие обозначения:

, .(6.7)

Тогда решениями приведенного уравнения (6.5) будут

;(6.8)

;(6.9)

,(6.10)

от которых заменой

(6.11)

снова можно перейти к решениям кубического уравнения (6.4).

3. Вычислим характеристические константы уравнения Ван-дер-Ваальса. Для удобства вычислений примем следующие единицы измерения: V - л/моль , P - атм, Т - К. Тогда R = 0,08206 л·атм/(моль·К);

a = 27·0,082062·6502/(64·31)=38,72 л·атм;

b = 0,08206·650/(8·31)=0,2151 л.

4. Давление насыщения находится методом последовательных приближений. В качестве первого приближения при Т = 400 К примем давление насыщения равным 10 атм.

5. Рассчитаем значения коэффициентов уравнения (6.4):

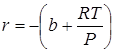= –(0,2151+0,08206·400/10) = – 3,4975;