Реферат: Квантовые свойства излучения

Иначе говоря, черное тело при любой температуре и частоте излучения является наиболее интенсивным источником излучения.

II. Если тело не поглощает излучения в какой-либо области спектра (aω = 0), то оно и не излучает в этой области спектра, т.е. rω = 0 (при данной температуре).

III. Зная спектр излучения черного тела при данной температуре () и зависимость монохроматического коэффициента поглощения данного тела от частоты (aω(ω)), можно найти спектр излучения тела rω(ω).

Интегральная форма закона Кирхгофа записывается для энергетической светимости во всем диапазоне частот:

Так как

, а для серых тел

и может быть вынесена за знак интеграла, то

,

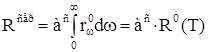где – энергетическая светимость черного тела.

Для данной температуры сильнее излучают те серые тела, которые обладают большим коэффициентом поглощения.

Законы теплового излучения черного тела (Стефана – Больцмана и Вина)

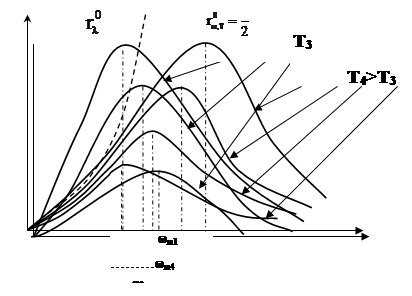
Экспериментально было установлено, что тепловое излучение черного тела имеет сплошной спектр. Схематические графики спектров для различных температур представлены на рисунке.

Из приведенных рисунков следует:

??? ??? r_ω ? r_λ . ?? ???????????????? ???? ?????, ? ??????? ???????????? r_{ω =} r_λ , ? ?? ????????? ????????? ? ?????? ?????? ???????, ??:

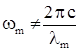
для каждой температуры существует максимум испускательной способности , который с увеличением температуры смещается в область бо'льших частот излучения (т.е. в область меньших длин волн);

т. к. энергетическая светимость черного тела 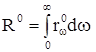равна площади под графиком rω0 (ω), то R0 увеличивается с повышением температуры (т.е. энергетическая светимость возрастает по мере нагревания черного тела).

Очень важная для характеристики теплового излучения величина – спектральная плотность энергетической светимости черного тела (испускательная способность), долгое время не могла быть вычислена теоретически, т. к. рассматривалась как классическая величина.

Рэлей и Джинс (1900 г) попытались обосновать экспериментальные зависимости с помощью классической статистической физики. Рэлей подошел к изучению спектральных закономерностей излучения черного тела с позиций статистической физики, а не термодинамики, как это делалось ранее. Он рассматривал равновесное излучение черного тела в замкнутой полости с отражающими стенками как совокупность пространственных электромагнитных стоячих волн. При этом колебания с различными частотами совершаются независимо друг от друга, и каждой частоте соответствует своя колебательная степень свободы. Рэлей применил к тепловому излучению закон классической статистической физики равномерного распределения энергии по степеням свободы, согласно которому на каждую степень свободы приходится энергия, равная kT. В частности, он предположил, что на каждое электромагнитное колебание в среднем приходится энергия, равная двум половинкам kT (одна – на электрическую, другая – на магнитную составляющую энергии волны). Таким образом, Рэлей и Джинс, считая среднюю энергию излучающего атомного осциллятора равной kТ, вывели формулу для спектральной плотности светимости черного тела:

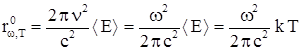(1)

Однако эта формула согласуется с экспериментами только в области малых частот и при высоких температурах. Для больших частот она явно неверна. Энергетическая светимость черного тела с учетом формулы Рэлея – Джинса

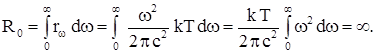
Невозможность обоснования законов излучения черного тела с помощью классической теоретической физики получило название "ультрафиолетовой катастрофы" (УФ – диапазону соответствуют малые длины волн λ и высокие частоты ω).

Теоретическое определение было получено М. Планком (1900 г), который отказался от установившегося положения классической физики о том, что энергия физической системы меняется непрерывно. Планк ввел понятие квантования излучения (поглощения) и сформулировал знаменитую гипотезу Планка: тела излучают (и поглощают) энергию не непрерывно, а дискретными порциями (квантами)

E = hν = ħωω = 2πν

h = 6,62·10-34 Дж·с – постоянная Планка; ħ = 1,054·10-34 Дж·с.

Представляя излучающее тело как совокупность гармонических атомов – осцилляторов, каждый их которых излучает квант энергии hν (ħω), Планк получил выражение для средней энергии осциллятора: 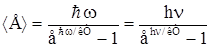, подставив которое в формулу Рэлея – Джинса, получим

.

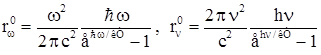Выражения для и , которые называют формулой Планка, блестяще согласуются с экспериментальными зависимостями. Используя соотношение между rν и rλ и формулу Рэлея – Джинса, получим формулу Планка для .

Так как