Реферат: Лабораторные работы по Основам теории систем
X3
К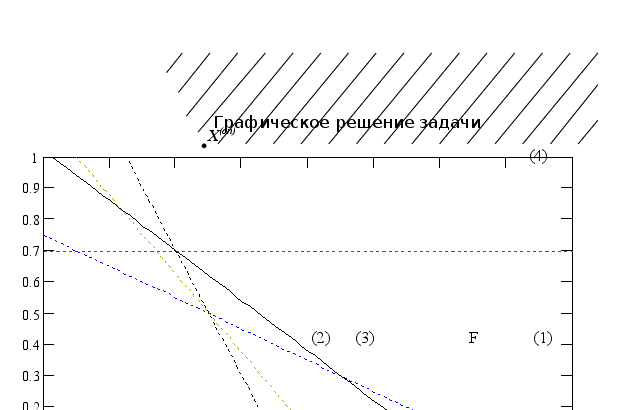
ритерий можно улучшить, т.к. 
, 
, но нельзя найти такое 
, при котором базисные переменные обращаются в 0. Значит задача неразрешима из-за неограниченности критерия.
5 вариант.
После отмеченного таким образом праздника обязательно наступает похмелье. Решим задачу из предыдущего варианта, минимизируя этот неприятный фактор, т.е. функция цели: 
.
Приводим ограничения к каноническому виду:
=> 
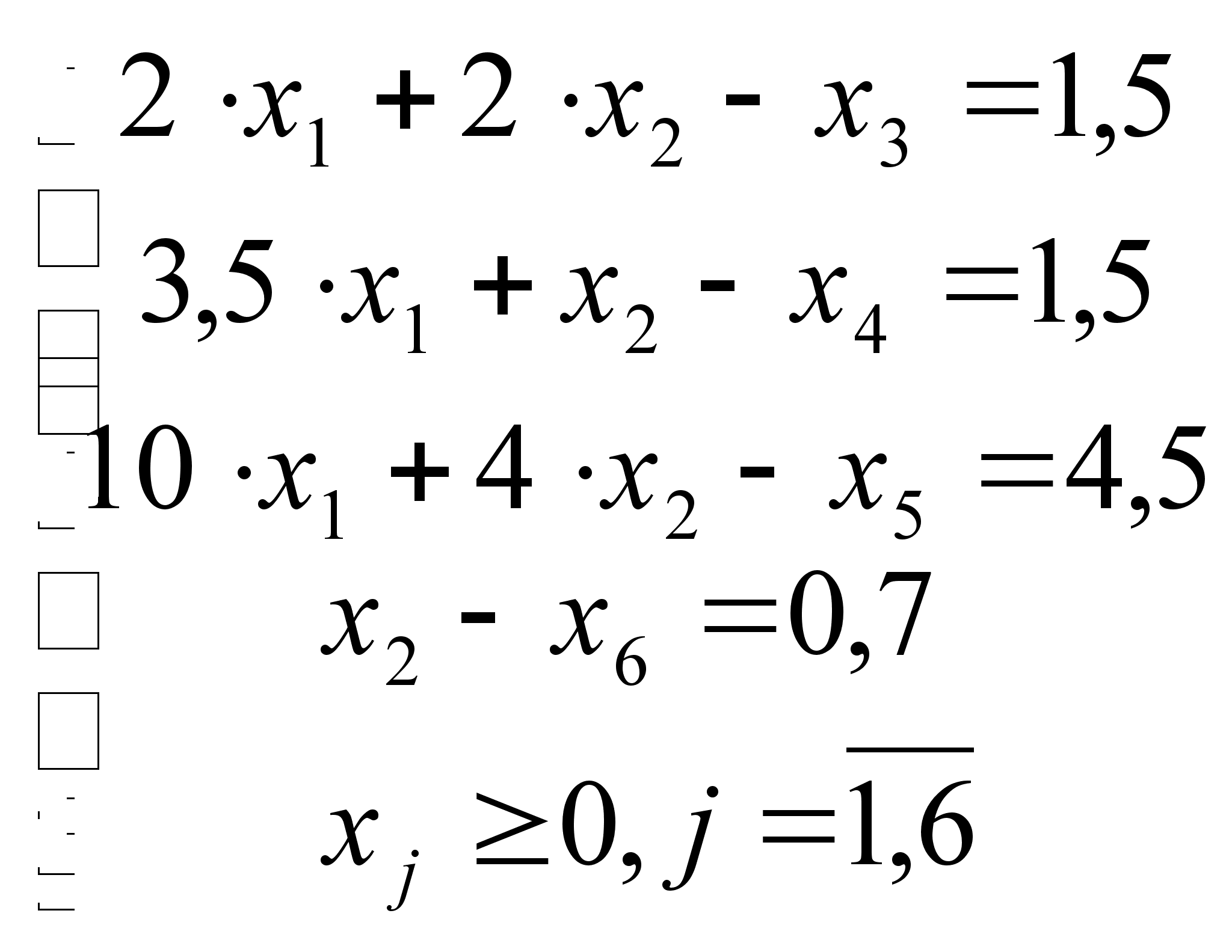
Эта задача решается методом искусственного базиса, т.к. в ней нет единичной подматрицы. Вспомогательная задача получается точно такой же, как и в предыдущем варианте, поэтому просто возьмем опорный план из предыдущей задачи.
;
-
16 10 0 0 0 0 Св
Б.П. X1
X2
X3
X4
X5
X6
в 0 X5
0 0 0 -2,85 1 -1,14 0,585 16 X1
1 0 0 -0,285 0 0,285 0,228 10 X2
0 1 0 0 0 -1 0,7 0 X3
0 0 1 -0,571 0 -1,42 0,357 F 0 0 0 -4,576 0 -5,424 3,648
Видим, что оценки свободных переменных меньше нуля, значит решение оптимальное.
; F = 3,648.
Д
елаем вывод: оптимальное решение может существовать и при неограниченности области.
Область не ограничена, но существует оптимальное решение 
, причем единственное, которое достигается в угловой точке.
Лабораторная работа № 3
Телешовой Елизаветы, гр. 726,
Теория двойственности в задачах линейного программирования.
Задача:
Для изготовления определенного сплава из свинца, цинка и олова используется сырье из тех же металлов, отличающееся составом и стоимостью.