Реферат: Лабораторные работы по Основам теории систем

Это решение является опорным, т.к. вектора условий при положительных компонентах решения линейно независимы, также , где , но не все оценки положительны (, где )

Опорный план является оптимальным, если для задачи максимизации все его оценки неотрицательны. не является оптимальным, значит критерий можно улучшить, если увеличить одну их отрицательных свободных переменных. Будем увеличивать , т.к. ее увеличение вызовет большее увеличение функции цели.

Предположим, что , тогда:

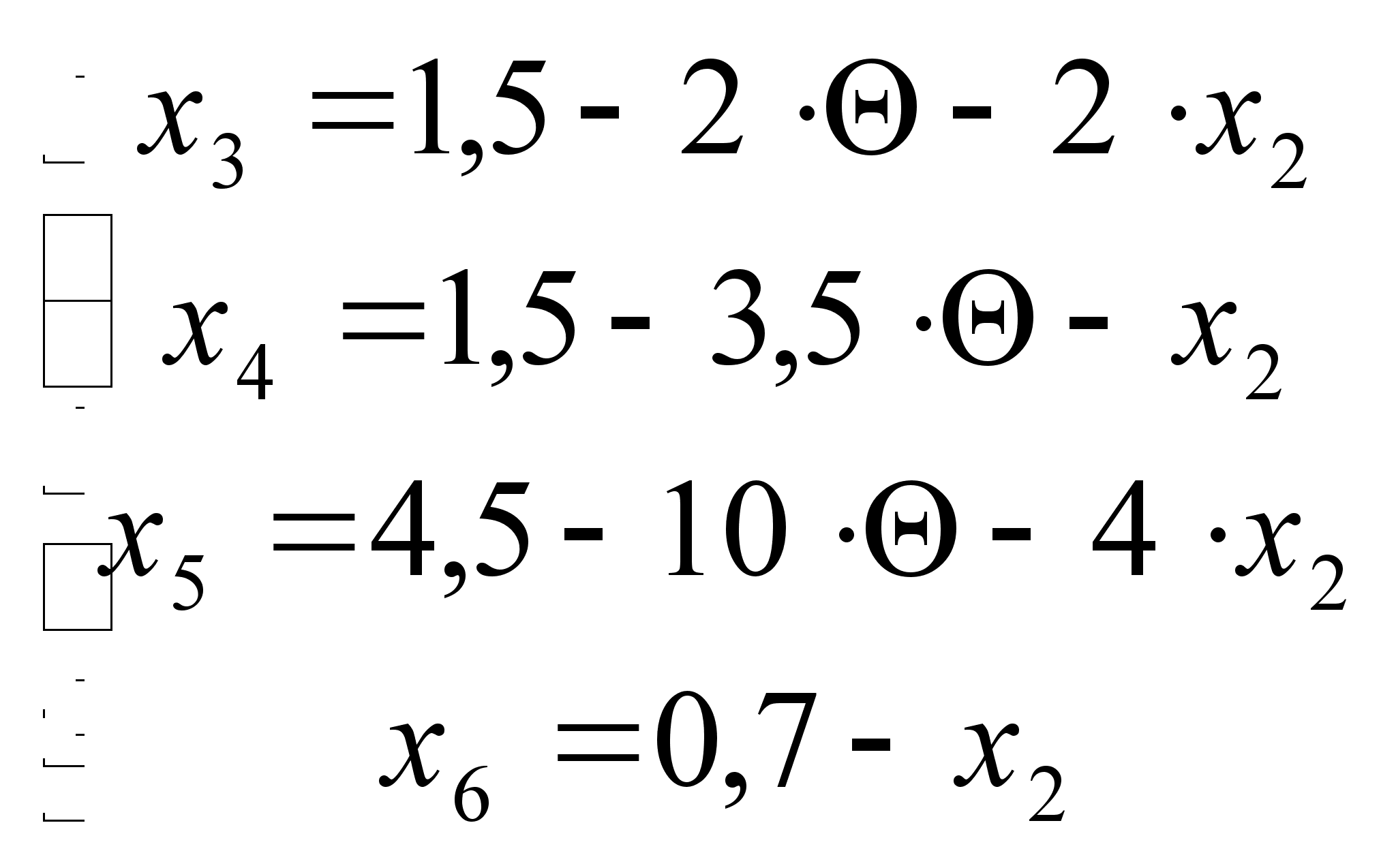
Запишем новый опорный план: . Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:

=>

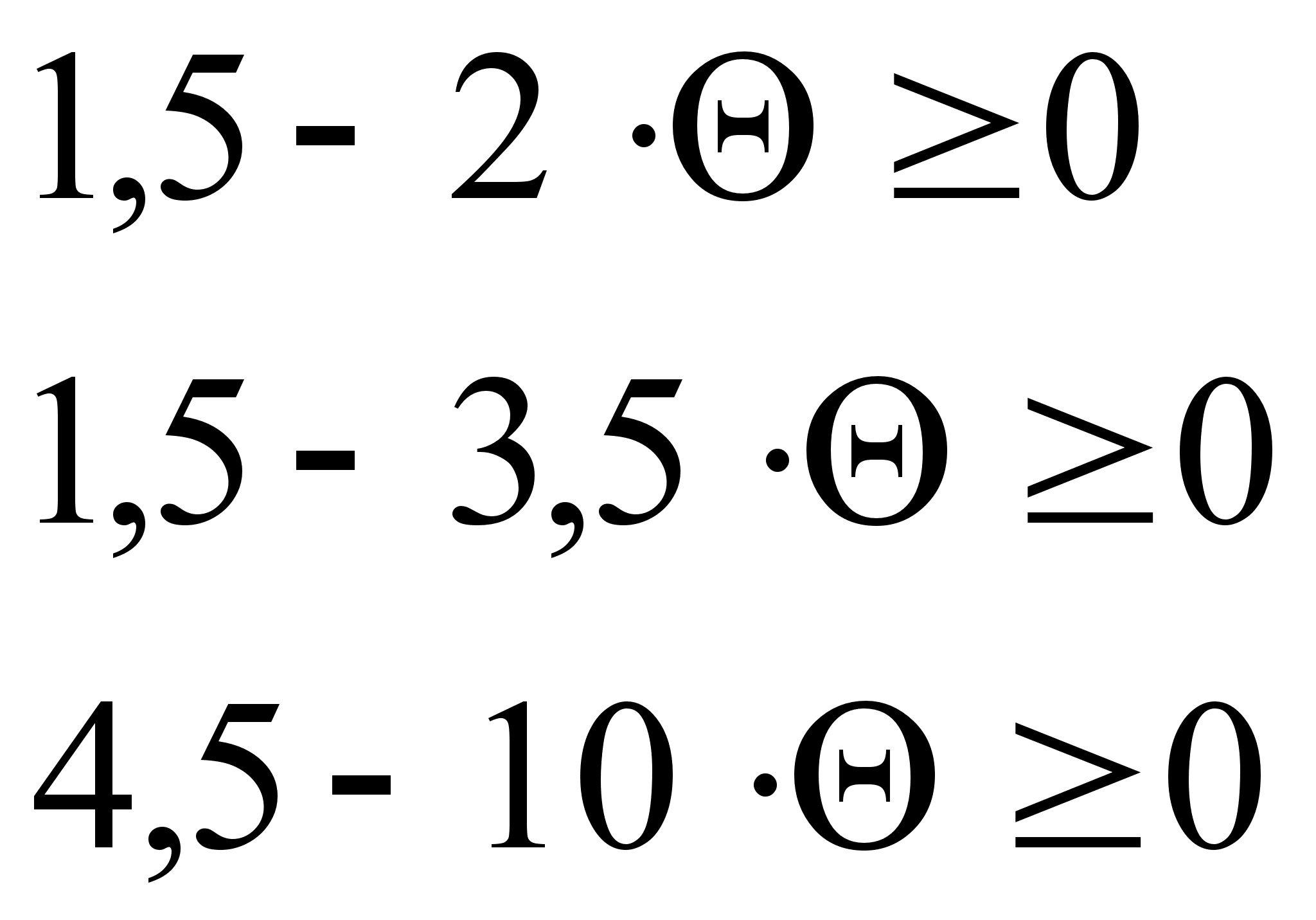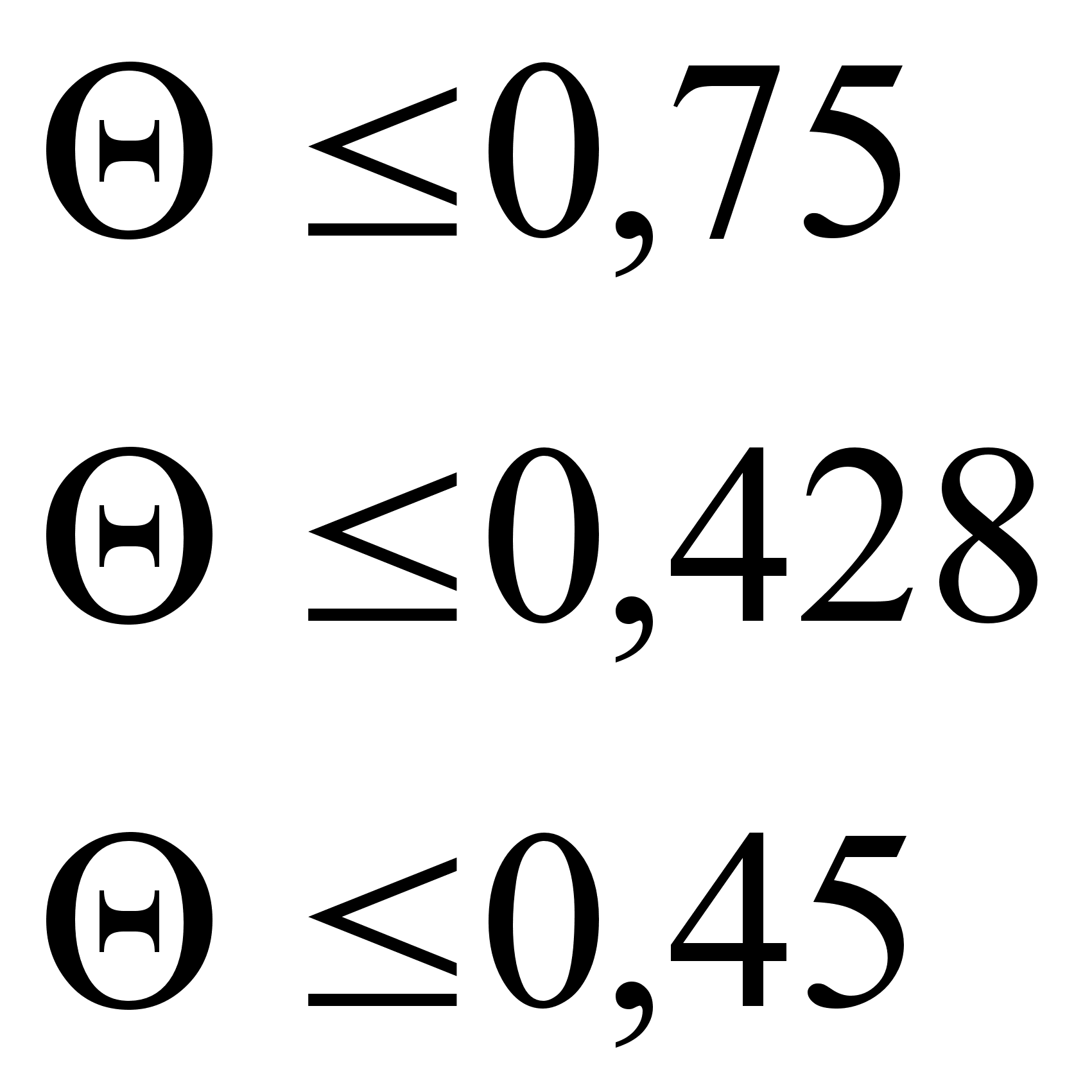
При увеличении , первой перестает выполнять условие неотрицательности переменная , т.к. она первая обращается в ноль. Значит выведем из базиса . Теперь базисными переменными являются , а свободными . Для анализа этого плана выразим функцию цели через новые переменные.

Из ограничения (2) имеем: .

Подставляя в функцию цели: получаем:

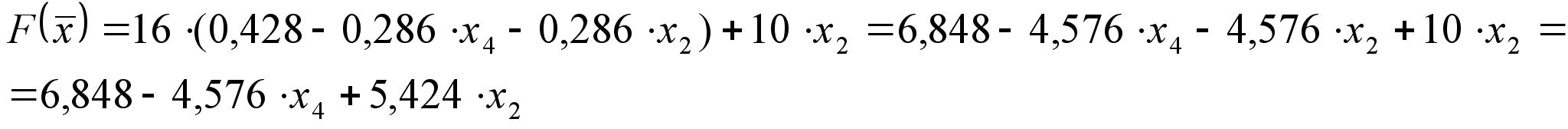
Оформим данный этап задачи в виде симплекс-таблицы:

Начальная симплекс-таблица:

		16	10	0	0	0	0
Св	Б.П.	X1	X2	X3	X4	X5	X6	в
0	X3	2	2	1	0	0	0	1,5
0	X4	3,5	1	0	1	0	0	1,5
0	X5	10	4	0	0	1	0	4,5
0	X6	0	1	0	0	0	1	0,7
	F	-16	-10	0	0	0	0	0

;

Пересчитаем элементы исходной таблицы по правилу четырехугольника:

		16	10	0	0	0	0
Св	Б.П.	X1	X2	X3	« 1 2 3 4 5 6 7 8 9 10 » К-во Просмотров: 720 Бесплатно скачать Реферат: Лабораторные работы по Основам теории систем >>> Скачать <<< Меню Поиск