Реферат: Лазерная система для измерения статистических характеристик пространственных квазипериодических структур
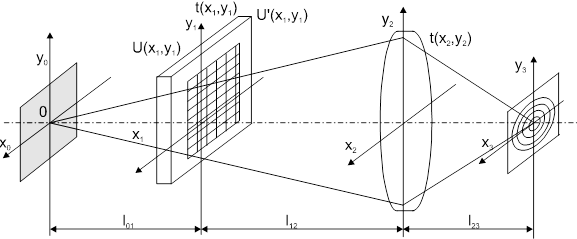
Рис.2. Схема КОС со входным транспарантом перед фурье-объективом
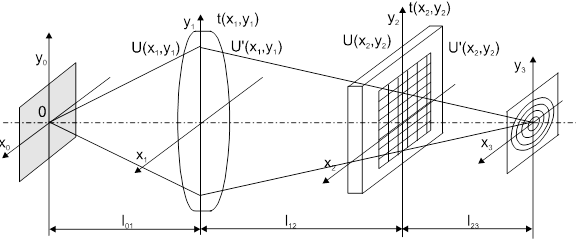
Рис.3. Схема КОС со входным транспарантом за фурье-объективом
3.Математическая модель квазипериодической
структуры СВЧ линий замедления
При статистических исследованиях геометрических размеров элементов пространственной структуры ЛЗ установлено, что из-за различных техноло-гических погрешностей, эти размеры являются величинами случайными с нормальным законом распределения. Таким образом, пространственная структура ЛЗ не является строго переодической, а поэтому ее энер-гетический спектр будет отличаться от энергетического спектра периоди-ческих структур.
Из скалярной теории [7, 8] известно, что оптической системой КОС в плоскости спектрального анализа формируется дифракционное изображе-ние пространственного объекта, помещенного во входной плоскости. Математические зависимости, описывающие форму дифракционного изоб-ражения, могут быть определены лишь путем решения задачи о дифракции когерентной световой волны на пространственной структуре объекта. Одна-ко для пространственной структуры ЛЗ с флуктуациями периодичности, решение такой задачи чисто оптическими методами не может быть полу-чено из-за значительной математической сложности ее. Кроме, того эти методы применимы лишь для решения дифракционных задач на регу-лярных детерминированных пространственных структурах и неприменимы для случайных пространственных сигналов.
Поэтому в настоящее время такие задачи для случайных оптических сигналов решают в оптике с применением методов статистической радио-физики в силу единства физических процессов и математических методов анализа прохождения электрических сигналов в электрических цепях и распостранения пространственных сигналов в оптических системах. Это позволяет определить распределение освещенности в дифракционном изображении квазипериодической пространственной структуры ЛЗ (т.е. ее энергетический спектр) путем вычисления усредненного квадрата преобра-зования Фурье над ее амплитудным коэфициентом пропускания.
Пространственная штриховая структура ЛЗ является квазипериодичес-ким сигналом, в технике ОСОИ, и состоит из взаимонезависимых прозрач-ных щелей и непрозрачных стенок. К тому же период пространственной структуры ЛЗ также является случайной величиной, так как он равен сумме двух взаимонезависимых величин. Таким образом, пространственная струк-тура ЛЗ относится к классу случайных квазипериодических сигналов.
Поскольку освещенность пространственной структуры ЛЗ, помещенной во входной плоскости КОС, равномерна по полю, то ее амплитудный коэфициент попускания 
может быть описан единично-нулевой функ-
цией. Поэтому, в пределах ширины 
прозрачных щелей функция 
, а в пределах ширины 
непрозрачных стенок, соответственно, 0. Кроме того, ширина щелей и стенок являются величинами взаимонезави-симыми, поскольку при изгибах стенок толщина их не изменяется, а изменяется лишь ширина щелей. Взаимонезависимость этих величин также возникает и потому, что зубья в верхней и нижней гребенках наре-заются раздельно на разных заготовках, после спаивания которых обра-зуются между зубьями щели, а ширина их уже не зависит от толщины зубьев, что подтверждается также малостью коэфициента корреляции 
для размеров и .
Фрагмент квазипериодической пространственной структуры ЛЗ и соот-ветствующая ему функция пропускания 
в сечении у=0 показаны на рис.4 (а и б), где Рх - период пространственной структуры, равный 
.
Поскольку ширина щелей и стенок являются величинами случайны-ми и взаимонезависимыми, то и период 
пространственной структуры ЛЗ будет также величиной случайной. Период является суммой двух случай-ных величин с нормальными законами распределения, следовательно, закон распределения также будет нормальным.
Таким образом, амплитудный коэфициент пропускания прост-ранственной квазипериодической структуры ЛЗ может быть описан функ-цией вида
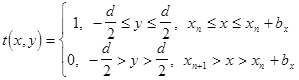(2.4), где 
- порядковый номер щели, 
- пространственная координата положения начала щели, 
- высота перекрытия зубьев в квазипериодической структуре ЛЗ.
Из выражения (2.4) видно, что переменные х и у функции взаимо-независимы, а поэтому эта функция является функцией с разделяемыми переменными, и может быть представлена в виде произведения функций 
и 
, т.е. 
(2.5).
В выражении (2.5) функция 
является финитной в пределах высо-ты перекрытия зубьев верхней и нижней гребенок пространственной структуры ЛЗ вдоль координаты х, как показано на рис.4б.
Для оптической системы КОС пространственная структура ЛЗ является квазипериодическим сигналом. В свою очередь, основными характеристи-ками такого сигнала, т.е. пространственной структуры ЛЗ, являются:
· средние размеры и ширины стенок и щелей, а также средние квадратические отклонения СКО 
и 
от них соответственно;
· законы распределения 
и 
размеров стенок и щелей;
· спектральная и корреляционная функции.
Для описания спектральных и корреляционных функций случайных сигналов часто используются характеристические функции. Характеристи-ческая функция 
случайной величины 
является фурье-образом ее закона распределения 
, т.е. 
, где 
- простран-ственная частота, измеряемая в [мм-1 ], поскольку в рассматриваемом случае координата является пространственной и имеет размерность [мм].
Тогда с учетом 
получим:
, а вводя замену переменных вида
. Этот интеграл в новых пределах интегрирования от 
до 
можно представить через элементарные функции следующим выражением
(2.6) , и аналогично 
(2.7).
Полученные выражения (2.6) и (2.7) являются характеристическими функциями квазипериодической пространственной структуры ЛЗ с нормаль-ным законом распределения ширины стенок и щелей.
Как в оптических, так и в электронных устройствах спектрального анали-за сигналов, существует возможность получения как амплитудного, так и энергетического их спектров. Однако в теории спектрального анализа пространственных сигналов известно, что при использовании квадратичес-ких фотодетекторов для регистрации параметров дифракционного изобра-жения, формируемого оптической системой КОС, автоматически на ее вы-ходе формируется энергетический спектр исследуемого сигнала. Парамет-ры такого спектра могут быть измерены соответствующими контрольно-измерительными приборами, а форма его определена с применением мето-дов статистической радиооптики путем интегрального преобразования Винера-Хинчина, либо на основе теоремы Хилли.