Реферат: Линейная теория и условия самовозбуждения автогенератора

Рис. 8.21. Структурная схема автогенератора

Восполнение потерь в схеме автогенератора осуществляется с помощью активного прибора (АП), к которому приложено напряжение свободных колебаний. Для компенсации потерь в колебательном контуре требуется, чтобы ток через активный прибор i _АП имел направление, указанное на эквивалентной схеме генератора (рис. 8.22).

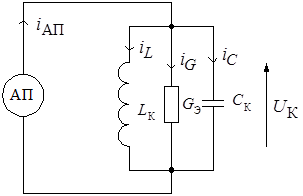
Рис. 8.22. Эквивалентная схема автогенератора

Изобразим активный прибор через его проводимость – G _АП и представим эквивалентную схему автогенератора (рис. 8.22) по переменному току в следующем виде (рис. 8.23):

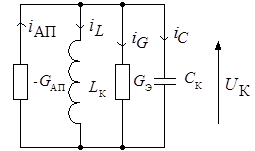
Рис. 8.23. Эквивалентная схема автогенератора по переменному току

Активный прибор обладает отрицательной проводимостью – G _АП < 0, что означает, что в контур вводится энергия, компенсирующая потери на активной составляющей проводимости колебательного контура G _Э . Отрицательную проводимость можно получить, как уже указывалось выше, шунтируя контур приборами, имеющими падающий участок на вольт-амперной характеристике (туннельным диодом, тиристором и т.д.), а также с помощью положительной обратной связи.

В схеме на рисунке 8.23 согласно первому закону Кирхгофа

где

Выразим токи через напряжение U _К , тогда

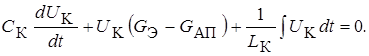(8.11)

Продифференцируем выражение (8.11) по t и разделим на С _К

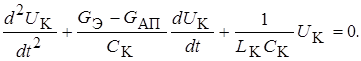(8.12)

Учитывая, что резонансная частота контура

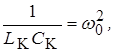
получим

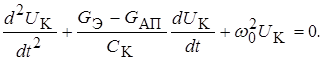(8.13)

Уравнение (8.13) получило название дифференциального уравнения автогенератора. Оно является нелинейным дифференциальным уравнением второго порядка, так как коэффициент при первой производной G _АП (крутизна вольт-амперной характеристики нелинейного элемента) зависит от переменной U _К и совпадает с дифференциальным уравнением колебательного контура (тема 3.1). В общем случае решения уравнений такого типа неизвестны. Существуют приближенные методы, позволяющие получить результаты с заданной степенью точности (особенно на ЭВМ). Следует однако иметь ввиду, что в начале зарождения колебаний амплитуда их очень мала и рабочая область на характеристике будет линейной, где бы не находилась рабочая точка. Это означает, что G _АП (крутизна вольт-амперной характеристики нелинейного элемента) не будет зависеть от U _К и дифференциальное уравнение окажется линейным. Общим решением такого уравнения (8.13) является временная зависимость напряжения на колебательном контуре:

(8.14)

где – частота свободных (затухающих) колебаний контура;

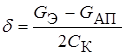– коэффициент затухания.

Амплитуда свободных колебаний, описываемых уравнением (8.14), определяется выражением и зависит от коэффициента затухания d. При d > 0 (рис. 8.24 а) свободные колебания в контуре будут затухающими, так как проводимость потерь превышает проводимость активного прибора (G _Э > G _АП ).

а) б) в)

Рис. 8.24. Амплитуда свободных колебаний при различных d

Если проводимость потерь G _Э компенсировать отрицательной вносимой проводимостью G _АП , то при d = 0 возникшие в контуре колебания будут продолжаться бесконечно долго, т.е. станут незатухающими (рис. 8.24 б). Если же по абсолютной величине вносимая отрицательная проводимость будет больше проводимости потерь (|G _АП | > G _Э ), то d > 0 и колебания в контуре будут нарастать (рис. 8.24 в), т.е. возникают условия самовозбуждения.

Таким образом, выявление условий самовозбуждения сводится к анализу генератора как линейной цепи и поэтому называется линейной теорией. При этом не обязательно составлять дифференциальное уравнение, а можно использовать известные методы анализа линейных цепей на устойчивость, так как нарушение устойчивости и есть самовозбуждение.