Реферат: Линейные устройства с дифференциальными операционными усилителями

где – алгебраическое дополнение матрицы.

Для одноканальных структур, когда источник сигнала подключается к первому каналу , а нагрузка – к последнему , достаточно минимизировать

(53)

с учетом ограничений, которые вытекают из предположения о пассивности коммутирующей части схемы:

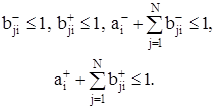(54)

Топологическую структуру алгебраического дополнения можно определить из известного правила Мэзона:

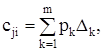(55)

где – k-й путь от входа схемы к выходу i-го активного элемента; – алгебраическое дополнение к k-му пути; m – число сквозных путей.

Учитывая, что

, (56)

а – является r-й комбинацией из q несоприкасающихся контуров, минимизация модуля дополнения возможна за счет применения контуров с положительным возвратным отношением и несоприкасающимися с указанным сквозным путем. Например, для двухкаскадного усилителя обеспечение разностных членов в Н₂ и F₂₂ возможно применением дополнительного контура , как это показано на рис. 6.

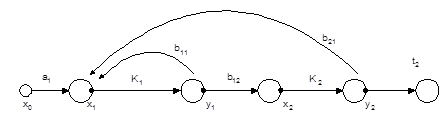
Рис. 6. Вариант структуры с минимальным влиянием второго каскада

В этом случае

(57)

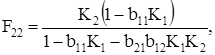(58)

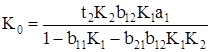. (59)

Следовательно, при осуществляется минимизация Н₂ и F₂₂ и, поэтому уменьшается влияние параметров, характеризующих неидеальность второго каскада. Если дополнительно потребовать

, (60)

то

. (61)

Таким образом, выполнение структурных и параметрических условий минимизации при надлежащем выборе глубины общей обратной связи не сопровождается уменьшением реализуемого коэффициента передачи. Использование такой связи не увеличивает влияние параметров первого каскада. Действительно,

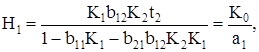(62)

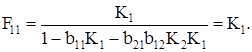(63)

Аналогично, введением дополнительного контура можно минимизировать влияние паразитных параметров первого каскада и, следовательно, получить структуру параметрически инвариантного усилителя или преобразователя. Принципиальная схема параметрически инвариантного двухкаскадного усилителя, реализующего настоящий принцип собственной компенсации, приведена на рис. 7.

Рис. 7. Принципиальная схема параметрически

инвариантного усилителя

Здесь

(64)

Покажем, что выполнение условий

(65)

приводит к достижению поставленной цели.

Из соотношений (59)–(63) следует

; (66)

(67)

. (68)

Таким образом, без потери усиления можно глобально экстремально минимизировать активную чувствительность, влияние дрейфа нуля и собственного шума второго активного элемента.

Полученные ранее соотношения не учитывали влияние составляющих, обратно пропорциональных произведению площадей усиления отдельных каскадов. Из алгоритма (18–20) знаменатель передаточной функции рассматриваемого усилителя будет иметь вид

(69)

где – постоянная времени i-го каскада.

Следовательно, условия устойчивой работы схемы нарушаются. Для восстановления устойчивости в схеме достаточно включить корректирующий конденсатор С_к . Тогда

(70)

где .

Поэтому

, (71)

и условие структурной устойчивости схемы восстанавливается.

Несложно показать, что при этом минимизируется чувствительность к и . Полученные условия параметрической инвариантности распространяются на случай произвольного числа каскадов, т.е. между первым и вторым каскадом можно дополнительно включить произвольное число усилителей, при этом их чувствительность будет равна нулю.

5. Базовый алгоритм структурного синтеза схем с собственной компенсацией

Выполненные исследования указывают на существование двух принципов собственной компенсации влияния параметров активных элементов на характеристики электронных устройств различного функционального назначения.

Первый принцип базируется на введении в структуру дополнительных компенсирующих контуров обратных связей, которые не изменяют способы конструирования коэффициентов идеализированных передаточных функций и поэтому не влияют на верхний уровень динамического диапазона схемы. Создание компенсирующих контуров предполагает соединение дифференциального входа активного элемента с дополнительным входом схемы, обладающим определенными функциональными особенностями. В этой связи для обеспечения однонаправленности передачи сигнала необходимо выполнить условие

, (72)