Реферат: Линейный гармонический осциллятор
Подставим найденные в (3.81) и (3.82) выражения гамильтониана в уравнение Шредингера (3.77) и перенесем постоянные множители в правую часть полученных уравнений :
 (3.83)
(3.83)
 (3.84)
(3.84)
3.5.8. Для выяснения смысла операторов ![]() и
и ![]() еще раз подействуем первым из них на обе части уравнения (3.83), а вторым – на уравнение (3.84), т.е. домножим эти уравнения слева на
еще раз подействуем первым из них на обе части уравнения (3.83), а вторым – на уравнение (3.84), т.е. домножим эти уравнения слева на ![]() и
и ![]() соответственно:
соответственно:
![]() , (3.85)
, (3.85)
![]() . (3.86)
. (3.86)
Подставим вместо произведений операторов (![]() ) и (
) и (![]() ) их выражения (3.82) и (3.81) и опять перенесем постоянные величины Ω в правую часть уравнений:
) их выражения (3.82) и (3.81) и опять перенесем постоянные величины Ω в правую часть уравнений:
 (3.87)
(3.87)
 . (3.88)
. (3.88)
В итоге каждое из уравнений (3.87) и (3.88) приобрело стандартный вид уравнения Шредингера, но собственные функции в них (![]() ) и (
) и (![]() ) отличны от волновой функции исходного состояния Ψ υ , а собственные значения
) отличны от волновой функции исходного состояния Ψ υ , а собственные значения ![]() отличаются от исходного ευ на постояннуювеличину. Функции (
отличаются от исходного ευ на постояннуювеличину. Функции (![]() ) отвечает уровень
) отвечает уровень ![]() , на величину 2Ω сдвинутый вниз по отношению к уровню состояния Ψ υ , т.е. оператор
, на величину 2Ω сдвинутый вниз по отношению к уровню состояния Ψ υ , т.е. оператор ![]() произвел понижение уровня на один номер:
произвел понижение уровня на один номер:
![]() . (3.89)
. (3.89)
Аналогично оператор ![]() сдвигает номер уровня и состояния Ψ υ на еди- ницу вверх:
сдвигает номер уровня и состояния Ψ υ на еди- ницу вверх:
![]() . (3.90)
. (3.90)
Функции ![]() и
и ![]() , полученные с помощью операторов
, полученные с помощью операторов ![]() и
и ![]() по формулам (3.89) и (3.90), не нормированы; но в дальнейших расчетах это несу-ественно. Состоянию
по формулам (3.89) и (3.90), не нормированы; но в дальнейших расчетах это несу-ественно. Состоянию ![]() отвечает уровень
отвечает уровень ![]() , а
, а ![]() – уровень
– уровень ![]() , т.е.
, т.е.
![]() . (3.91)
. (3.91)
3.5.9. Переход к обычной энергетической шкале с использованием подста-новок (3.74б и 3.74в) дает
![]() . (3.92)
. (3.92)
Согласно формуле (3.92), уровни гармонического осциллятора эквидис-тантны , и интервал между.ними равен ![]() .
.
3.5.10. Продолжая исследование лесенки уровней, учтем, что сверху она неограничена, но нижняя граница определена уровнем основного состояния Ψ0 , ниже которого не существует состояний системы. Поэтому попытка подействовать оператором понижения ![]() на волновую функцию основного состояния должна дать нулевой результат, т.е. применительно к волновой функции основного уровня оператор понижения сыграет роль ее “уничтожителя” – аннигилятора:
на волновую функцию основного состояния должна дать нулевой результат, т.е. применительно к волновой функции основного уровня оператор понижения сыграет роль ее “уничтожителя” – аннигилятора:
![]() (3.93)
(3.93)
Здесь целесообразно вернуться к переменной х . С учетом выражения для ![]() (3.80) и подстановки (3.74а) формулу (3.93) после простых преобразований приводим к дифференциальному уравнению для
(3.80) и подстановки (3.74а) формулу (3.93) после простых преобразований приводим к дифференциальному уравнению для ![]() :
:
 , (3.94)
, (3.94)
при интегрировании которого получим волновую функцию основного состояния:
 . (3.95)
. (3.95)
Далее находим нормировочный множитель А0 :
 (3.96)
(3.96)
 . (3.97)
. (3.97)
При раскрытии выражения (3.96) использован интеграл Пуассона:
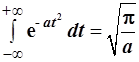 .
.