Реферат: Логические системы в различных функциональных наборах и их реализация

При этом каждый класс полностью определяется любым его представителем. Сопоставив результаты исследования с результатами пункта 3.2 получим следующие зависимости

М1 Ì K1	М2 Ì K1	М3 Ì K2	М5 Ì K1	М6 Ì K2
М1 Ì K3	М2 Ì K2	М5 Ì K2	М6 Ì K3
М5 Ì K3

или

K₁ = M₁ È M₂ È M₅

K₂ = M₂ È M₃ È M₅ È M₆

K₃ = M₁ È M₅ È M₆

Результаты исследования занесены в таблицу 3. Результаты исследования на эквивалентность и толерантность необходимы для оптимизации построения логической схемы.

3.4. Матрица эквивалентности и толерантности.

Матрицу эквивалентности и толерантности можно представить в виде квадрата, по диагонали которого строятся классы эквивалентности, а затем устраиваются отношения толерантности. Матрица эквивалентности и толерантности представлена в таблице 4.

Матрица эквивалентности и толерантности. Таблица 4.

3.5. Диаграмма Эйлера.

Диаграмма Эйлера дает наглядное представление о том, как распределяются признаки по классам толерантности и эквивалентности. Диаграмма Эйлера для выбранных ФАЛ представлена на рисунке 3.5.

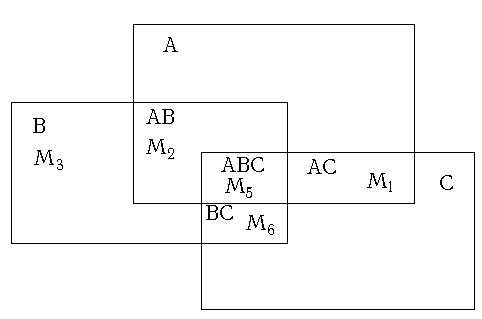
Диаграмма Эйлера. Рис. 3.5

3.6. Построение комбинационной схемы.

Комбинационная схема автомата распознавания набора признаков H = {h₁ , h₃ , h₅ } построена на основе результатов исследований в пункте 3.1 и пункте 3.4.

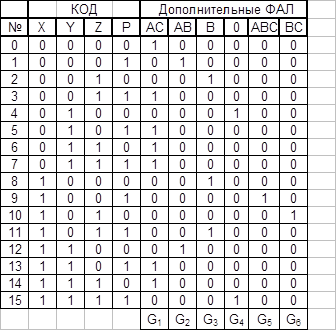
Таблица 5

Используя таблицу 5, можно записать следующие отношения:

G₁ = (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) = (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZ) Ú (YZP)

G₂ = (XYZP) Ú (XYZP)

G₃ = (XYZP) Ú (XYZP) Ú (XYZP)

G₄ = (XYZP) Ú (XYZP)

G₅ = (XYZP)

G₆ = (XYZP)

Тогда ФАЛ можно представить в виде:

F₁ = G₁ Ú G₂ Ú G₅

F₃ = G₂ Ú G₃ Ú G₅ Ú G₆

F₅ = G₁ Ú G₅ Ú G₆

Эти отношения эквивалентны ФАЛ в СДНФ, полученным в пункте 2.5.

Комбинационная схема строилась в два этапа:

1 этап: - построение комбинационной схемы на элементах и, или,

(нестандартных).