Реферат: Математические методы методы

Общей задачей линейного программирования называется задача, которая состоит в определении максимального или минимального значения функции

, при условиях

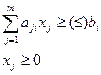a, c, b – заданные величины.

Функция f называется целевой , а условия ограничения b_i – ограничениями линейной задачи.

Совокупность чисел x=( x₁ , x₂ ,…, x_j ) удовлетворяющих ограничениям задачи называется допустимым решением (планом).

План x* , при котором целевая функция принимает максимальное/минимальное значение, называется оптимальным планом .

Для решения исходной задачи, имеющей вид «» можно преобразовать ограничения равенства в добавлениях его левой части дополнительной неотрицательной переменной, а ограниченное неравенство «» преобразовать в равенство вычитанием из его левой части дополнительной неотрицательной переменной.

Свойство основной задачи линейного программирования

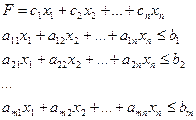
- запись задачи линейного программирования в векторной форме

- план задачи линейного программирования.

План X называется опорным планом основной задачи линейного программирования, если положительные коэффициенты стоят при линейно-независимых векторах P_j .

Опорный план называется невыраждебным , если он содержит ровно m положительных компонент, в противоположном случае он называется выраждебным.

Базисный вектор состоит из значений целевой функции и коэффициентов целевой функции. Для того, чтобы план был оптимальным необходимо, чтобы выполнялось равенство

Опорный план X является оптимальным, если для любого j

Для нахождения оптимального плана составляют симплекс-таблицу. Чтобы проверить будет ли исходный план оптимальным просматривают элементы m+1 строки.

В ней может иметь место 1 из 3 случаев:

1. для j= m+1, m+2… m+ n

2. и меньше 0 все соответствующие этому индексу величины a_ij <0 .

3. для некоторых индексов J и для каждого такого J по крайней мере одно из чисел a_i <0.

[таблица]

Транспортная задача

Математическая постановка задачи

Постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления A₁ , A₂ ,…, A_m в n пунктов назначения B₁ , B₂ ,…, B_n . В качестве критерия оптимальности берется минимальная стоимость перевозок, либо минимальный объем времени доставки. Тарифы перевозок из пункта i в пункт j обозначаются C_ij (стоимость перевозок единицы груза).

- целевая функция.

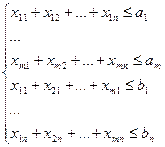
При решении транспортной задачи следует учитывать, что обратные перевозки исключаются.

Планом транспортной задачи называется неотрицательное решение системы ограничений.

План, при котором целевая функция принимает минимальные значения, называется оптимальным планом транспортной задачи.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--