Реферат: Математические методы методы

,

т.е. общее количество запасов равно общему количеству потребностей, то модель такой транспортной задачи называется закрытой.

Задачи нелинейного программирования

Общий вид. Эта задача состоит в том, чтобы определить максимальное/минимальное значение функции F от переменной f( x₁ , x₂ ,…, x_n ) , при условии, что все переменные удовлетворяют соотношениям:

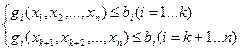
f_i , g_i – некоторые функции и переменные

b_i – некоторое фиксированное число

Результатом решения задачи будет x=( x₁ , x₂ ,…, x_n ) , координаты которой удовлетворяют данным соотношениям. Эти соотношения образуют системе ограничений и включают в себя условия неотрицательности переменных.

В отличии от задачи линейного программирования, функция f может быть функцией степенной (квадратной, кубической и т.д.).

Графический способ решения задачи линейного программирования:

1. Найти область допустимых решений задачи, используя систему ограничеий;

2. Построить график функций f ;

3. Определяют границы допустимых решений;

4. Находят точку области допустимых значений через которую проходит график функций f и определяют в ней значение функции.

Метод множества Лагранжа

Рассмотрим частный случай общей задачи нелинейного программирования.

Предполагается, что система ограничений содержит только уравнения, отсутствуют условия неотрицательности переменных и функции f и g_i непрерывные вместе со своими частными производными.

Для решения задачи выводят набор переменных , называемых множителями Лагранжа и составляют функцию Лагранжа

Далее находят частные производные и рассматривают систему из n+ m переменных.

,

Всякое решение системы уравнений определяет точку , в которой может иметь место экстремум функции .

Алгоритм решения задачи:

1. Составить функцию Лагранжа;

2. Найти частные производные от функции Лагранжа и прировнять их к 0;

3. Решить систему уравнений, найдя точки, в которых целевая функцию может иметь экстремум;

4. Среди точек, подозрительных на экстремум находят такие, в которых достигается экстремум и находят значение функции в них.