Реферат: Математическое моделирование технологических операций механической обработки поверхностей деталей лезвийными инструментами (Учебное пособите по курсу: математическое моделирование технологических операций-4834)

Кроме того, формообразование номинальной поверхности детали как огибающей семейства поверхности резания может быть осуществлено двумя способами. При последовательном выполнении движения - резания и подач и одновременном. Если в процессе формообразования одновременно изменяются

параметры движения резания и подач (одной или нескольких), то результирующее рабочее движение режущей кромки называют сложным движением резания. При последовательном выполнении движений кромка выполняет указанное выше простое движение резания при неизменности параметров подач, которые изменяются при осуществлении последующего движения формообразования в направлениях подач.

Для формообразования номинальной поверхности детали безразлично, какое движение резания осуществляет инструмент - простое или сложное. Но в то же время, формы поверхностей резания, образованные при простом и сложном, движении режущей кромки, будут несколько отличаться друг от друга и в соответствии о этим будут отличаться размеры срезаемых слоев припуска. Однако известно, что это отличие является практически незначительным и им обычно пренебрегают при расчетах схем резания. В работе [2] сделана численная оценка этого изменения, которая подтверждает его не существенность даже для оценки технической шероховатости поверхности, определяемой пересечением поверхностей резания.

Для формообразования произвольной номинальной поверхности безразлично, является ли траектория точек контакта о номинальной поверхностью ее образующей или простей криволинейной координатной линией g (или n), так как в том и другом случае должно существовать движение, определяющее формирование соседнего семейства поверхностей резания по второй криволинейной координатной линии п. Единственным отличиям этих вариантов формообразования является лишь то, что в первом случае движение формообразования будет непрерывным, и во-втором прерывным последовательным, т.е. необходимо обратно-поступательное движение инструмента и последовательное выполнение подачи по линии координаты.

Из изложенного следует, что для универсального математического моделирования различных процессов формообразования поверхностей инструментами необходимо и достаточно рассмотреть процесс формирования произвольной поверхности детали на базе универсальной кинематической схемы. Осуществить ориентацию детали так, чтобы обрабатываемая поверхность имела контакт с режущей кромкой произвольной формы в общей точке 0 двух систем координат ХоYоZо и X2Y2Z2 (рис. 7). Формируемую поверхность считать заданной двумя линиями криволинейных координат g n п или ее образующей. Рассматривать произвольную номинальную поверхность детали следует как огибающую семейств огибаемых произвольных поверхностей резания. Так как погрешность, связанная с заменой сложного результирующего движения резания и формообразования на составляющие незначительна, то любое элементарное движение, указанное на универсальной кинематической схеме может быть выбрано за абсолютное движение резания. Перемещения, необходимые для формообразования произвольной поверхности детали, определяются временем последовательного контакта, режущей кромки с теоретически заданной поверхностью детали при ее огибании, поэтому безразлично в какой последовательности режущей кромкой могут быть выполнены перемещения в направлении всех движений универсальной схемы. Так как при сложном результирующим движении все перемещения режущей кромки выполняются одновременно, то необходимо установить связь между величинами перемещений и длительности цикла формообразования по

времени. Временем (т) может быть величина определяющая последовательный выход и вход режущей кромки или кромок в контакт о теоретической формируемой поверхностью при образовании последовательно: пары

18

формообразующих поверхностей резания в одном из семейств поверхностей и пары соседних семейств.

Согласно свойства вращательных и поступательных движений твердого тела, уравнение перемещений любой точки тела является общим законом движения в пространстве. Поэтому для вывода уравнения произвольных поверхностей резания необходимо и достаточно записать закон перемещения контактной точки О, прилежащей произвольной линии режущей кромки, при выполнении ею всех движений универсальной кинематической схемы последовательно. Для анализа процесса формообразования поверхности при существовании сложного результирующего движения резания необходимо определить абсолютное движение резания и достаточно установить связь между величинами отдельных перемещений, если это движение неопределенно.

В универсальной кинематической схеме (рис 7) будем считать заданной произвольную номинальную поверхность двумя линиями ее образующей и направляющей. В исходной момент формообразования точка контакта двух системХ2Y2Z2 и ХоYоZо принадлежит теоретически заданной поверхности детали. Для формообразования произвольной поверхности как огибающей

семейства огибаемых поверхностей резания достаточно, чтобы за время (т) точки О, принадлежащая режущей кромке, завершив движение по траектории резания снова стала принадлежать формируемой поверхности или любой из двух линий, например ее образующей.

Будем считать, что при существовании Zu режущих кромок инструментом является фреза, у которой точки всех кромок в сечении плоскостью Y202Х2 расположены через центральный угол ф=2п/Zu. Тогда за время т примем отрезок времени, соответствующий повороту системы инструмента X2Y2Z2 вокруг оси O2Z2 на центральный угол ф. Обозначим перемещения по направлениям движения, указанных на универсальной схеме,

за время т:

Поворот системы X2Y2Z2 по стрелке А на угол ф=2п/Zu

Поворот системы ХоYоZо по стрелке Б на угол Q=ф*п2/nu

Перенос начала системы координат X2Y2Z2 относительно осей

Где nu и пd - числа оборотов в минуту системы:

Х2Y2Z2 вокруг оси O2Z2 и ХоYоZо вокруг оси 02Х2 соответственно: Sг(х), Sг(у), Sz(2) - перемещения в расчете мм/зуб вдоль осей системы Х2У2Z2.

Общее уравнение поверхностей резания может быть представлено последовательной записью систем параметрических уравнений.

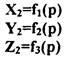- параметрическое уравнение режущей кромки в контактном положении в системе координат инструмента

(1)

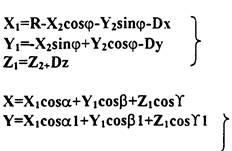
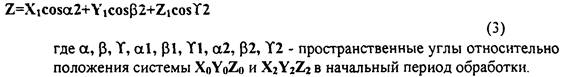
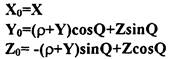
(5)

Таким образом, по уравнению (5) можно рассчитать координаты (ХоYoZо) точек поверхности или семейства поверхностей резания, относящиеся к исх?