Реферат: Матричная форма формулы Крамера

Рассмотрим систему линейных алгебраических уравнений (СЛАУ ), содержащую
т уравнений и п неизвестных:

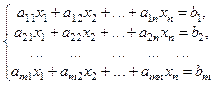(1)

Пусть

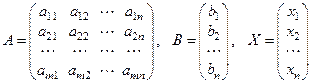
– матрица коэффициентов при неизвестных, столбец свободных членов (чисел стоящих справа от равенства в системе (1)) и столбец неизвестных соответственно системы (1). Матрица А называется основной матрицей системы (1). Тогда очевидно, что система (1) может быть кратко записана в матричной форме . Форма (1) называется координатной записью системы.Если , т.е. число уравнений равно числу неизвестных, то СЛАУ называется «квадратной », она принимает вид:

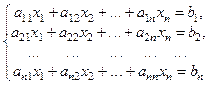(2)

Если же матрица А к тому же не вырождена, т.е. , то тогда СЛАУ (2) можно решить как матричное уравнение по формуле

. (3)

Этот метод называется матричным способом решения СЛАУ (2).

Пример. Решить систему матричным способом, если это возможно:

Решение . Запишем эту систему как матричное уравнение , где
, . Вычисляем: , следовательно, матричный способ применим. Находим обратную матрицу:

Следовательно,
.

Ответ:

Формулы Крамера для решения СЛАУ

Эти формулы применимы для решения СЛАУ при тех же условиях, что и матричный способ, а именно, когда матрица А коэффициентов при неизвестных этой СЛАУ квадратная и не вырожденная . Для нахождения неизвестных квадратной системы (2) надо вычислить главный определитель , убедиться что , и затем вычислить п вспомогательных определителей , где определитель () получается из главного определителя заменой в нем k -го столбца на столбец В свободных членов:

Тогда решением системы (2) будет: .

Вывод формул Крамера . Распишем подробно формулу (3) .

Вспомним, что , где – алгебраическое дополнение элемента , равное , а – определитель порядка , полученный из главного определителя D вычеркиванием i -й строки и j -го столбца. Получим

.

Итак, матричный способ дает формулу

(4)

Сравним эту формулу с выражением для , полученным по формуле Крамера:

. (5)

Заметим, что у всех элементов k -го столбца этого определителя алгебраические дополнения точно такие же, как и у элементов k -го столбца матрицы А . Поэтому, разложив определитель в (5) по этому столбцу, получим:

. (6)

Полученная формула (6) в точности совпадает с (4). Формулы Крамера доказаны.

Пример. Решить систему методом Крамера, если это возможно:

Решение . Вычислим главный определитель системы: , следовательно, метод Крамера применим. Далее вычислим три вспомогательных определителя:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--