Y
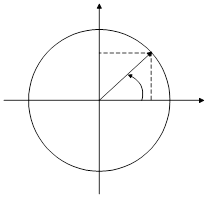
Определение 1. Синусом угла 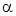 называется отношение ординаты
называется отношение ординаты 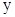 конца подвижного радиус-вектора
конца подвижного радиус-вектора 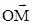 , который образует угол
, который образует угол 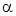 с осью абсцисс, к длине этого радиус-вектора и обозначается
с осью абсцисс, к длине этого радиус-вектора и обозначается 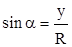 .
.
Определение 2. Косинусом угла  называется отношение абсциссы
называется отношение абсциссы  конца подвижного радиус-вектора
конца подвижного радиус-вектора 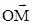 , который образует угол
, который образует угол 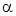 с осью абсцисс, к длине этого радиус-вектора и обозначается
с осью абсцисс, к длине этого радиус-вектора и обозначается 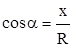 .
.
Определение 3. Тангенсом угла 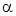 называется отношение ординаты
называется отношение ординаты 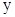 конца подвижного радиус-вектора
конца подвижного радиус-вектора 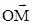 , который образует угол
, который образует угол 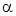 с осью абсцисс, к абсциссе
с осью абсцисс, к абсциссе 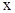 конца этого радиус-вектора и обозначается
конца этого радиус-вектора и обозначается 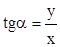 .
.
Определение 4. Котангенсом угла 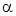 называется отношение абсциссы
называется отношение абсциссы 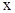 конца подвижного радиус-вектора
конца подвижного радиус-вектора 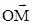 , который образует угол
, который образует угол 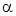 с осью абсцисс, к ординате
с осью абсцисс, к ординате 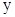 конца этого радиус-вектора и обозначается
конца этого радиус-вектора и обозначается 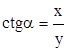 .
.
Из приведенных определений следует, что
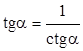 ,
, 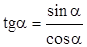 ,
, 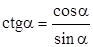 ,
,
причем у единичной окружности
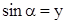 ,
, 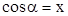 .
.
Введение произвольных по знаку и абсолютной величине углов позволяет каждому действительному числу 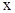 поставить в соответствие угол в
поставить в соответствие угол в 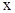 радиан и, наоборот, каждому углу - однозначно определяемое действительное число, равное числу радиан. Такое взаимнооднозначное соответствие позволяет определить тригонометрические функции числового аргумента.
радиан и, наоборот, каждому углу - однозначно определяемое действительное число, равное числу радиан. Такое взаимнооднозначное соответствие позволяет определить тригонометрические функции числового аргумента.
Определение 5. Тригонометрическая функция числа 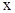 это та же тригонометрическая функция угла величиной в
это та же тригонометрическая функция угла величиной в 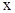 радиан .
радиан .
Рассмотрим графики основных элементарных тригонометрических функций.
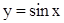
.
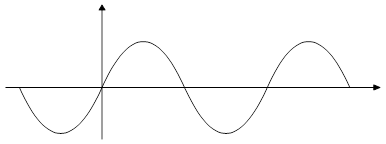
Здесь
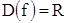 ;
; 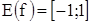 ;
;
период 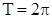 ;
; 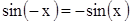 ; корни
; корни  , где
, где  .
.
К-во Просмотров: 772
Бесплатно скачать Реферат: Мера угла

![]() называется отношение ординаты
называется отношение ординаты ![]() конца подвижного радиус-вектора
конца подвижного радиус-вектора ![]() , который образует угол
, который образует угол ![]() с осью абсцисс, к длине этого радиус-вектора и обозначается
с осью абсцисс, к длине этого радиус-вектора и обозначается ![]() .
.![]() называется отношение абсциссы
называется отношение абсциссы ![]() конца подвижного радиус-вектора
конца подвижного радиус-вектора ![]() , который образует угол
, который образует угол ![]() с осью абсцисс, к длине этого радиус-вектора и обозначается
с осью абсцисс, к длине этого радиус-вектора и обозначается ![]() .
.![]() называется отношение ординаты
называется отношение ординаты ![]() конца подвижного радиус-вектора
конца подвижного радиус-вектора ![]() , который образует угол
, который образует угол ![]() с осью абсцисс, к абсциссе
с осью абсцисс, к абсциссе ![]() конца этого радиус-вектора и обозначается
конца этого радиус-вектора и обозначается ![]() .
.![]() называется отношение абсциссы
называется отношение абсциссы ![]() конца подвижного радиус-вектора
конца подвижного радиус-вектора ![]() , который образует угол
, который образует угол ![]() с осью абсцисс, к ординате
с осью абсцисс, к ординате ![]() конца этого радиус-вектора и обозначается
конца этого радиус-вектора и обозначается 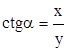 .
.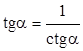 ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.![]() поставить в соответствие угол в
поставить в соответствие угол в ![]() радиан и, наоборот, каждому углу - однозначно определяемое действительное число, равное числу радиан. Такое взаимнооднозначное соответствие позволяет определить тригонометрические функции числового аргумента.
радиан и, наоборот, каждому углу - однозначно определяемое действительное число, равное числу радиан. Такое взаимнооднозначное соответствие позволяет определить тригонометрические функции числового аргумента.![]() это та же тригонометрическая функция угла величиной в
это та же тригонометрическая функция угла величиной в ![]() радиан .
радиан .
![]() ;
; ![]() ;
; ![]() ;
; ![]() ; корни
; корни ![]() , где
, где ![]() .
.