Реферат: Мера угла

Дисциплина: "Высшая математика"

Тема: "Мера угла"

1. Градусная и радианная мера угла

Как было показано ранее, функция задает определенное соотношение между двумя числовыми множествами. Однако в некоторых случаях область определения функции может являться множеством чисел, имеющих размерность. В частности, речь идет о множестве значений некоторого угла. Прежде чем приступить к рассмотрению подобных функций, напомним некоторые факты, связанные с измерением углов.

Определение 1. Углом в называется центральный угол, опирающийся на дугу окружности, имеющей длину, равную ее части.

Исторически сложилось деление градуса на 60 минут, а минуты на 60 секунд, то есть: , . Секунды делятся на десятые, сотые и т.д. части. Градус является наиболее распространенной единицей измерения углов.

Определение 2. Углом в 1 радиан называется центральный угол, опирающийся на дугу окружности, имеющую длину, равную ее радиусу .

Таким образом, для отыскания радианной меры центрального угла достаточно длину дуги (l), на которую он опирается, разделить на длину радиуса (R), то есть .

Из сказанного выше следует, что полной окружности будет соответствовать в градусах угол в 360 раз больший, то есть . В радианах это будет радиан. Необходимо также отметить, что величина угла в градусной и радианной мере никак не связана с радиусом окружности. Следовательно, в дальнейшем можно рассматривать окружность любого радиуса, проще всего - единичного.

Формулы перехода от градусной меры дуг и углов к радианной и наоборот имеют вид:

, .

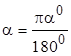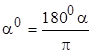Отсюда следует, что

1 рад = 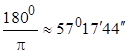, а рад0,01745 рад.

Рассмотрим теперь координатную плоскость с началом координат в точке О. Проведем окружность единичного радиуса с центром в точке О и отметим точки ее пересечения с осями координат.

Рассмотрим произвольную точку M на окружности и вектор , который называется радиус-вектором точки M.

Будем рассматривать центральные углы AOM, образованные векторами и при перемещении точки M по окружности.

Y

D

C

B

A

O

X

M

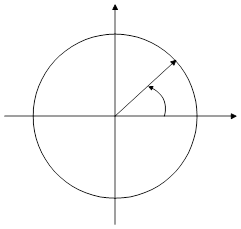
Если точка M совпадает с точкой A, то полагают равным нулю. Будем считать положительным, если вращение вектора от начального положения происходит в направлении противоположном движению часовой стрелки. В противном случае будем считать отрицательным.

Так как полный оборот вектора приводит его в то же положение, однозначно определить величину угла, если это не оговорено, нельзя. Иначе говоря, в общем случае

Или

.

2. Элементарные тригонометрические функции произвольного угла

--> ЧИТАТЬ ПОЛНОСТЬЮ <--