Реферат: Метод хорд

Пользуясь рекуррентной формулой (2) и формулой для оценки точности вычисления, составим процедуру уточнения корня методом хорд:

Procedure chord(a, b, eps, min : real; var x : real);

Здесь x:=x1-((b-x1)*fx(x1))/(fx(b)-fx(x1)) – рекуррентная формула,

abs(fx(x))/min < eps – формула для оценки точности вычислений.

При вычислении производной функции

Function proizv(x0, eps : real) : real;

будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева на равном расстоянии от - точке, в которой мы хотим найти производную.

Таким образом, вычисляется производная в середине промежутка.

По значениям f' можно таким же способом найти производную от f', т.е. f''. Можно выразить f'' непосредственно через f(x):

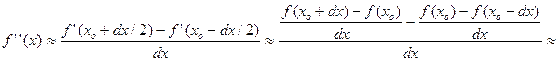
Для производной третьего порядка можно использовать следующую формулу:

Здесь dx:=1 - первоначальная величина промежутка,

dx:=dx/2 – для уточнений делим промежуток на 2,

dy:=fx(x0+dx/2 -fx(x0-dx/2) – вычисление первой производной в точке x0 ,

dy2:=fx(5*x0/4+dx)-2*fx(5*x0/4)+fx(5*x0/4-dx) – вычисление второй производной, для определения точности вычисления, используется вторая производная в точке

abs(dy2/(2*dx))<eps - формула для оценки погрешности

дифференцирования,

proizv:=dy/dx – значение первой производной.

Для оценки точности вычисления корня необходимо вычислять наименьшее значение производной f'(x) на промежутке [a, b], поэтому надо найти производную в точке x0.

Так как мы вычислили значение производной, то составим процедуру определения модуля ее наименьшего значения на промежутке [a, b]:

Procedure minimum(a,b,eps:real;var min:real);

Для этого достаточно сравнить модуль значения производной на концах промежутка и выбрать среди этих двух значений меньшее. Это можно сделать , так как по условию, функция на промежутке строго монотонна вместе со своими производными первого и второго порядков. Следует брать значение очень близкое к a, но справа от нее, аналогично для точки b - брать близкое значение слева от b, так как если в точке a или b производная будет равна нулю, тогда деление на нуль станет невозможным и в программе будет получена ошибка.

Здесь min:=abs(proizv(a,eps))- модуль значения производной функции в начале отрезка,

d:=abs(proizv(b,eps))- модуль значения производной функции в конце отрезка,

If min>d Then – сравнение значений модуля производной.

Функция для указания точности вычисления: