Реферат: Метод последовательных уступок Теория принятия решений

а все К_r квазивогнуты. При этих условиях множество стратегий, удовлетворяющих ограничениям r) задачи (1), также выпукло (r=1,2, ..., S), так что каждая из задач 1), 2),..., S) является задачей квазивогнутого программирования. Если Ks строго квазивогнут, то решением задачи S) может служить лишь единственная и потому эффективная стратегия; если же |при этом U замкнуто и ограничено, а все К_r непрерывны на U, то любая максимизирующая последовательность, являющаяся решением S), эффективна.

Пример 3. Предположим, что из многогранника U задачи, описанной в примере 1, удалена вся грань А'В'С', но оставлена точка В. Теперь эта точка оказывается единственным решением 3) задачи (1). Здесь точка В, конечно, эффективна. Любая сходящаяся к ней последовательность внутренних точек многогранника, удовлетворяющих ограниче­ниям задачи 3), будет максимизирую щей для Ks, но не будет эффективной. Указанное положение — следствие не замкнутости рассматриваемого в данном примере множества U.

В связи с тем, что не всегда стратегия, получен­ная с помощью метода последовательных уступок, является эффективной, возникает и такой вопрос: обязательно ли среди множества стратегий, выде­ляемых этим методом, существует хотя бы одна эффективная?

В общем случае на этот вопрос положительный ответ дать нельзя, однако имеет место такое утверждение: если UÌRⁿ — множество замкнутое и ограниченное, а все К_r непрерывны, то решением S) задачи (1) служит по крайней мере одна эффективная стратегия.

Действительно, при выполнении условий этого утверждения множество U^s стратегий-решений S) оказывается непустым, замкнутым и огра­ниченным. Следовательно, существует точка u*ÎU^S , в которой функция достигает наибольшего на U^s значения. Нетрудно убедиться в том, что u* эффективна.

Таким образом, при решении почти всякой при­кладной многокритериальной задачи метод последо­вательных уступок выделяет в качестве оптималь­ных и эффективные стратегии. Однако необходимо отметить, что выделенные эффективные стратегии не обязаны быть эквивалентными (см. пример 1); но нетрудно проверить, что это возможно лишь при S³3.

Если нельзя гарантировать, что при решении рассматриваемой многокритериальной задачи метод последовательных уступок приводит к получению лишь эффективных стратегий (в частности, если по выполняется вышеприведенное условие единст­венности), то для выделения эффективной страте­гии среди решений задачи S) достаточно, как пока­зывает только что проведенное доказательство,

найти 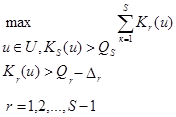(2)

Однако практически более удобно применять такой прием : заменить в S) критерий K_s на ,

где À — положительное число;

в результате получится задача:

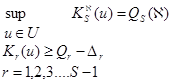(3)

Нетрудно доказать, что любая стратегия, являющаяся решением задачи (3), эффективна; более того, всякая максимизирующая последовательность, служащая решением этой задачи, также эффективна.

Смысл указанного приема заключается в том, что при достаточно малом числе À>0 для любой полученной в результате решения задачи (3) стратегии w значение критерия K_S (w) будет весьма близким к Q_s ^*) и эта стратегия эффективна, в то время как при решении S) задачи (1) может быть получена стратегия и, которую выгодно заме­нить некоторой эффективной стратегией v>u, су­щественно лучшей, чем и, но одному или даже не­скольким частным критериям. А поскольку величи­ны уступок А, на практике устанавливаются при­ближенно, то замена Ks на K*_s при малых À>0 в силу указанной причины оказывается допустимой и оправданной.

Таким образом, понятие эффективной стратегии позволило уточнить вычислительную процедуру отыскания оптимальных стратегий методом после­довательных уступок.

С другой стороны, метод последовательных уступок позволяет указать характеристическое свойство эффективных стратегий.

Теорема 1.

Для любой эффективной стратегии u* существуют такие числа D^* _r , что эту стратегию можно выделить методом последовательных уступок, т. е.
при D_r= D^* _r , r=1, 2,...,S—1, стратегия u* являет­ся единственным (с точностью до эквивалентности) решением S) задачи (1).

Теорема 1 характеризует эффективные стра­тегии с помощью последовательности задач (1). В частности, она показывает, что метод последова­тельных уступок можно использовать для построе­ния множества эффективных стратегий.

Более того, теорема 1 позволяет исследовать и сам метод последовательных уступок. Действи­тельно, она показывает, что при любом фиксирован­ном расположении частных критериев, по степени относительной важности одним лишь выбором ве­личин уступок можно обеспечить выделение любой эффективной стратегии в качестве оптимальной (так что проблема отыскания оптимальной страте­гии, т. е. проблема выбора эффективной стратегии из всего множества U°, формально эквивалентна проблеме назначения надлежащих величин уступок при произвольном фиксированном упорядочении критериев).

Следовательно, для решения многокритериаль­ной задачи нужно так ранжировать критерии, чтобы потом удобнее было выбирать величины уступок. Учитывая вышеизложенное и внимательно рассмо­трев порядок назначения величин уступок, можно сделать следующий вывод: метод последовательных уступок целесообразно применять для решения тех многокритериальных задач, в которых все частные критерии естествен­ным образом упорядочены по степени важности, причем каждый критерий настолько существенно более важен, чем последующий, что можно ограни­читься учетом только попарной связи критериев и выбирать величину допустимого снижения очеред­ного критерия с учетом поведения лишь одного сле­дующего критерия.

Особенно удобным является случай, когда уже в результате предварительного анализа многокритериальной задачи выясняется, что можно допустить уступки лишь в пределах «инженерной» точности (6—10% от наибольшей величины критерия).

Решение многокритериальной задачи методом последовательных уступок — процедура довольно трудоемкая, даже если заранее выбраны величины всех уступок. Поэтому большой интерес представляет вопрос: можно ли при заданных D_i получить оптимальную стратегию за один этап, сведя после­довательность задач (1) к одной экстремальной задаче?

Мы можем указать лишь приближенный способ одноэтапного решения для S=2. Он основан на следующем утверждении:

Лемма 1.

Пусть множество UÌR^p замкнуто и ограничено, K₁ и К₂ непрерывны на U, D₁ ³0 и À£D₁ /M¹ ₂ , где

(4)

Тогда для любой стратегии u*, доставляющей функции L=K₁ +ÀК₂ наибольшее на U значение, справедливо неравенство Q₁ -K₁ (u*)£D₁ причем если K₁ (u*)£ Q₁ , то