Реферат: Метод последовательных уступок Теория принятия решений

ПЛАН

Введение	3
Суть метода последовательных уступок	4
Порядок решения детерминированных многокритериальных задач методом последовательных уступок	5
Исследование метода последовательных уступок	9
Список использованной литературы.	19

ВВЕДЕНИЕ

Вопросы принятиянаилучших (оптимальных) решений стали в настоящее время весьма актуаль­ными,особенно в экономике, технике,военном деле и других областях человеческой деятельности.

Задачи отысканиянаилучших (илихотя бы удовлетворительных) путей достижения поставленных целей являются основными в новом разделе нау­ки— исследовании операций, — который тесно свя­зан с различными математическими дисциплинами, в том числе теорией игр,математическим программированием и теориейоптимальных процессов, теорией вероятностей и многими другими.

СУТЬ МЕТОД А ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК

Процедура решения многокритериальной задачи методом последовательных уступок заключается в том, что все частные критерии располагают и нумеруют в порядке их относительной важности; максимизируют первый, наиболее важный критерий; затем назначают величину допустимого снижения значения этого критерия и максимизируют второй по важности частный критерий при условии, что значение первого критерия не должно отличаться от максимального более чем на величину установленного снижения (уступки); снова назначают величину уступки, но уже по второму критерию и находят максимум третьего по важности критерия при условии, чтобы значения первых двух критериев не отличались от ранее найденных максимальных значений больше чем на величины соответствующих уступок; далее подобным же образом поочередно используются все остальные частные критерии; оптимальной обычно считают любую стратегию, которая получена при решении задачи отыскания условного максимума последнего по важности критерия.

Таким образом, при использовании метода последовательных уступок многокритериальная задача сводится к поочередной максимизации частных критериев и выбору величин уступок. Величины уступок характеризуют отклонение приоритета од них частных критериев перед другими от лексикографического: чем уступки меньше, тем приоритет жестче.

ПОРЯДОК РЕШЕНИЯ ДЕТЕРМИНИРОВАННЫХ МНОГОКРИТЕРИАЛЬНЫХ ЗАДАЧ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК

При решении многокритериальной задачи мето­дом последовательных уступок вначале производит­ся качественный анализ относительной важности частных критериев; на основании такого анализа критерии располагаются и нумеруются в порядке убывания важности, так что главным является критерий K₁ , менее важен. K₂ , затем следуют остальные частные критерии К₃ , К₄ ..., K_S . Максимизируется первый по важности критерий K₁ и определяется его наибольшее значение Q₁ . Затем назначается величина «допустимого» снижения (уступки) D₁ >0 критерия K₁ и ищется наибольшее значение Q₂ второго критерия K₂ при условии, что значение первого критерия должно быть не меньше, чем Q₁ —D₁ . Снова назначается величина уступки D₂ >0, но уже по второму критерию, которая вместе с пер­вой используется при нахождении условного макси­мума третьего критерия, и т. д. Наконец, максими­зируется последний по важности критерий Ks при условии, что значение каждого критерия К_r из S—1 предыдущих должно быть не меньше соответствую­щей величины Q_r —D_r ; получаемые в итоге страте­гии считаются оптимальными.

Таким образом, оптимальной считается всякая стратегия, являющаяся решением последней задачи из следующей последовательности задач:

1) найти Q₁ =

(1)

2) ????? Q₂ =

………………………………..

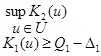
3) найти Q_S =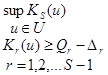

Если критерий K_S на множестве стратегий, удов­летворяющих ограничениям задачи S), не достигает своего наибольшего значения Q_s , то решением мно­гокритериальной задачи считают максимизирую­щую последовательность стратегий {u^k } из указан­ного множества (lim K_S (u^k ) = Q_S ).

k->¥

Практически подобные максимизирующие после­довательности имеет смысл рассматривать и для то­го случая, когда верхняя грань в задаче S) дости­гается, так как для решения экстремальных задач широко применяются итеративные методы.

Величины уступок, назначенные для много­критериальной задачи, можно рассматривать как своеобразную меру отклонения приоритета (степени относительной важности) частных критериев от жесткого, лексикографического.

Величины уступок D_r последовательно назнача­ются в результате изучения взаимосвязи частных критериев.

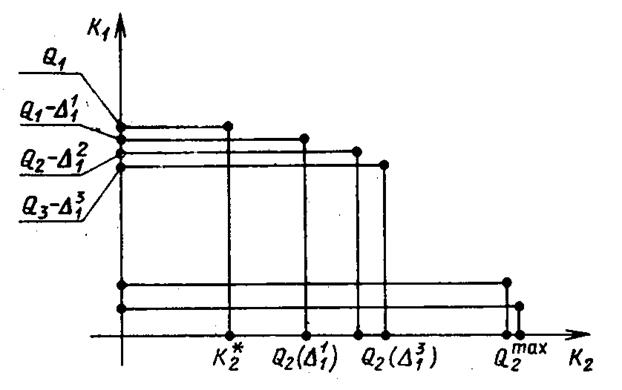
Вначале решается вопрос о назначении величи­ны допустимого снижения D_r первого критерия от его наибольшего значения Q₁ . Практически для это­го задают несколько величин уступок D¹ ₁ , D² ₁ , D³ ₁ … и путем решения 2) в задаче (1) определяют соответствующие макс. значения Q₂ (D¹ ₁ ), Q₂ (D² ₁ ), Q₂ (D³ ₁ ), и второго критерия. Иногда, если это не слишком сложно, отыскивается функция Q₂ (D₁ ). Результаты расчетов для наглядности Представляем графически (Рис 1)

Рис 1

Он показывает, что вначале даже небольшие величины уступок позволяют получить существенный выигрыш по вто­рому критерию; с дальнейшим увеличением уступки выигрыш растет все медленнее. На основе анализа полученных данных и решают вопрос о назначении величины уступки D₁ , а затем находят Q₂ (D₁ ).

Далее рассматривают пару критериев K₂ и K₃ вновь назначают «пробные» величины уступок Q₂ (D² ₂ ), , ... и, решая 3) в задаче (1), отыскивают наибольшие значения третьего критерия Q₃ (D¹ ₂ ), Q₃ (D² ₂ ),... Полученные данные анализируют, назначают D₂ , переходят к следующей паре критери­ев К₃ , K₄ и т. д.

Наконец, в результате анализа взаимного влия­ния критериев K_S-1 и K_S выбирают величину по­следней уступки D_S-1 и отыскивают оптимальные стратегии, решая S) в задаче 1 (обычно ограничива­ются нахождением одной такой стратегии).

Таким образом, хотя формально при использо­вании метода последовательных уступок достаточно решить лишь S задач (1),однако для назначе­ния величин уступок с целью выяснения взаимосвя­зи частных критериев фактически приходится ре­шать существенно большее число подобных задач.

ИССЛЕДОВАНИЕ МЕТОДА ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК

Во введении при изучении отношения предпоч­тения ³, порождаемого векторным критерием, бы­ло выяснено, что в качестве оптимальных вообще могут выступать лишь эффективные стратегии. По­этому возникают естественные вопросы: всегда ли использование метода последовательных уступок приводит к получению эффективных стратегий, а если не всегда — то в каких случаях (при выпол­нении каких условий) можно гарантировать полу­чение лишь эффективных стратегий?

Оказывается, что метод последовательных усту­пок не всегда приводит к выделению лишь эффек­тивных стратегий, т. е. решениями S) из задачи (1) могут быть и неэффективные стратегии. Это легко подтвердить простым примером.

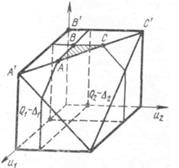
Пример 1. Пусть множество U Ì R³ — многогранник, изображенный на рис.2 , K₁ (u)=u1, K₂ (u)=u_2, K₃ (u)=u₃ . Здесь решением 3 из задачи (1) является любая точка треугольника ABC (на рисунке он заштрихован), но эффек­тивны лишь точки отрезка АС.

Справедливо, однако, утверждение: если u* — единственная (с точностью до эквивалентности) стратегия, являющаяся решением S) из задачи (1), то она эффективна.

Действительно, предположим, что стратегия u* неэффективна, так что существует стратегия u'>u*. Но стратегия u' также удовлетворяет всем огра­ничениям S) задачи (1) и доставляет кри­терию K_S значение Q_s ; иначе говоря, u' оказыва­ется решением этой зада­чи, что противоречит ус­ловию единственности u*. Утверждение доказано.

Рис 2

Можно доказать так­ же, что если UÌRⁿ за­мкнуто и ограничено, К_r непрерывны на U, а стратегия, являющаяся реше­нием S) задачи (1), единственна с точностью до эквивалентности, то любая максимизирующая последовательность, служащая решением S), эффективна.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--