Реферат: Метод Зойтендейка

Точка х является точкой Ф. Джона для и сходной задачи тогда и только тогда, когда опти мальное значение целевой функции задачи поиска направле ния равно нулю.

??????????????. ??????????? ???????? ??????? ??????? ? ???????????????? ?????? ?????????? ??????????? ????? ???? ? ??? ? ?????? ? ??? ??????, ???? ??????? ?????????? ??? ?? и ???? ???????. ?? ??????? ??? ????, ????? ??? ??????? н ? ????? ???????, ???????и ?? ? ??????????, ????? ??????в ????? ????? ????? u_o ? u_i , , ???

Это и есть условие Ф. Джона.

Алгоритм метода Зойтендейка (случай нелинейных ограничений-нерав енств)

Начальный этап. Выбрать начальную точку х₁ , для которой g_i (x_i )£0 при i= 1, ..., m. Полож ить k= 1 и перейти к ос­новному этапу.

Основной этап. Шаг 1. Положить и ре­шить следующую задачу:

Пусть ( z_k , d_k ) — оптимальное решени е. Если z_k =0, то остано­виться; x_k является точкой Ф. Джона. Если z_k < 0, то перейти к шагу 2.

??? 2. ????? ? ???????? ^ ??????????? ??????? ????????? ?????? ?????????? ???????????:

где. Положить . заменить k на k+ 1 и перейти к шагу 1.

??????. ?????????? ??????

Решим эт у задачу методом Зойтендейка. Начнем процесс из точки .Отметим, что

Итерация 1

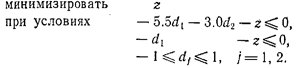????? ???????????. ? ????? х ₁ = (0.00, 0.75) ^T и ???? ? ????????? ????ксов активных ограничений есть I= { 3}. ??? ???? ?????? ?????????? н ?????????? ????? ???

Можно легко проверить, используя симплекс-метод, что оптимальным решением этой задачи является вектор

Ли нейный поиск. Любая точка по направлению d ₁ == (1.00, —1.00)^T из точки x_i = (0.00, 0.75) ^T может быть представлена в виде ,а соответствующее ей значение целевой функци и равно . Макси­мальное значение, для которого остается допустимой точкой, равно == 0.414. При этом значении l активным ста­новится ограничение . Значение l получается из решения следующей задачи одномерной ми нимизации:

минимиз ировать 6l² —2.5l—3.375

при условии 0£l£0.414

Оптимальное значение равно l ₁ = 0.2083. Следовательно, х ₂ = (x₁ + l₁ d₁ ) -( 0.2083,0.5417)^T .

Итерация 2

Поиск направления. В точке x₂ = (0.2083, 0.5417) ^T имеем ( х₂ )= (— 4,2500, —4.2500) ^T Активных ограничений в этой точке нет, и поэтому задача определения направления имеет вид

минимизировать z

при условиях —4.25d₁ —4.25d₂ —z£ 0,

-1< d₁ <1, j =1, 2.

Оптимальным решением является вектор d₂ =(1, 1) ^T , а z₂ = -8.50.

Линейный поиск. Можно легко проверить, что мак­ симальное l, при котором точка x₂ +ld₂ допустима, равно l_max == 0.3472. При этом активным становится ограничение . Значение l₂ получается минимизацией при условии и, оче­видно, равно l₂ = 0.3472, так что х_з = х ₂ +l ₂ d₂ = (0.5555, 0.8889)^T .

Итерация 3

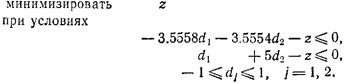????? ???????????. ? ????? x_з = (0,5555, 0.8889)^T и ???? (?_з )= (?3.5558, ?3.5554)", ? ????????? ???????? ???????? ?????????и ? ???? I ={1}. ?????? ??????????? ??????????? ????? ???

Оптимальным решением является вектор.

Лин ейный поиск. Максимальное значение l при котором точка x _з + l d_з допустима, равно l_max = 0,09245. При этом l ак­ти вным становится ограничение . Значение l₃ полу­чается минимизациейпри условии 0,09245. Оптимальным решением этой за­дачи являетсяl₃ = 0.09245, так что = (0.6479, 0.8397)^T .

Итерация 4

Поиск, направления. Для точки х₄ = (0.6479, 0.8397) ^T имеем =(— 3 .0878, —3.9370)^ а I ={2}. Задача определения направления имеет вид

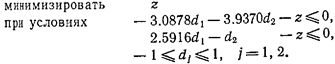Оптимальным решением этой задачи является вектор d₄ = (-0.5171, 1.0000) ^T и z₄ = — 2.340.

Линейный поиск. Максимальное значение К , для которого точках₄ + ld₄ допустима, равно l _{m ах} = 0.0343. При этом огра­ничение становится активным. Значение l₄ полу­чается минимизацией f (x₄ + ld₄ ) == 3,569l ² — 2.340l —6.4681 при условии и равно l ₄ = 0.0343. Следовательно, новой точкой является x₅ == x₄ + l₄ d₄ = (0.6302, 0.8740)^T .Значе­ ние целевой функции в этой точке равно -6.5443, т. е. сравня ю со значением —6.5590 в оптимальной точке (0.658872, 0.808226)^T .

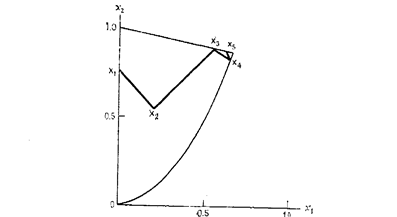
В табл. 2 приведены результаты вычислений на первых четырех итерациях метода. На рис. 7 показан процесс поиска оптимума.

Таблица 2

Рис 7

Учет нелинейных ограничений-равенств