Реферат: Метод Зойтендейка

Чтобы быть более точным, рассмотрим следующую задачу:

минимизировать f (х)

при условиях g_i (х)£0, i= 1,..., m,

h_i (х)= 0, i =1, ...,i.

????? x_k ??????????? ????? ? l= { i. g_i (?_k )== 0}. ????? ?????????? ?????? ????????? ??????м ?????????:
??????? ??????????? d_k ???????? ??????????? ? ?????????????-?????????? ? ? ????????? ???????? ???и ?????? ?????????????-????????????. ???????? ????? ????? d_k н ??????????? ??????????? ? ?????????? ??????? ???????? ? ????? х _k+1 , ????? ???? ??????? ???????????.

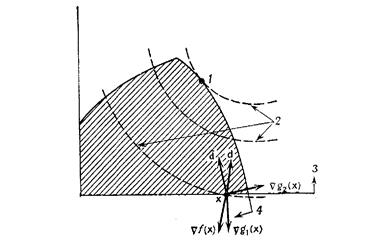
Рис. 9. Использование поч ти активных ограничений. 1 — опти мальное решение; 2— линии уровня целевой функции; 3—1-е ограничение; 4— 2-е ограничение.

Использование почти активных огран ичений

Напомним задачу определения направлени я как для случая ли­ нейных, так и нелинейных ограничений-неравенств. Если задан­ная точка близка к границе, определяемой одним из ограниче­ний, и если это ограничени е не используется в процессе нахож­дения направления движения, то может случиться так, что удастся сделать только маленький шаг и мы окажемся на гра­нице, определяемой этим ограничением. На рис. 9 в точке х активным является только первое ограничение. Однако точка х близка к границе, определяемой вторым ограничением. Если м ножество I в задаче определения направления задать в виде I ={ 1}, то оптимальным будет направление d и до выхода на границу допустимой области можно сделать только маленький шаг. Если же в множество активных ограничений включить оба ограничения, т. е. положи ть I={1, 2) , то решение задачи Р

определения направления даст вектор и , который обеспечивает большие возможности для движения в рамках допустимой об­ласти. Таким образом, это н аводи т на мысль о том, что в ка­честве множества I следует брать совокупность индексов почти активных ограничений. Точнее, вместо множества { i: g_i (х)= 0} в качестве I следует брать множество { i ,g_i (х)+е ³0}, где е>0—достаточно малое чи сло. Метод возможных направлений не обязательно сходится к точке Ф. Джона. Это

следует из того, что соответствующее алгоритмическое отображение незамкнуто. При более формальном использовании введённого здесь понятия почти активного ограничения можно установить замкнутость алгоритмического отображения и, следовательно, сходимость общего алгоритма.

Список литературы:

1. М. Базара, К. Шеттл «Нелинейное программирование. Теория и алгоритмы» М.: Мир 1982

2. Д. Химмельблау «Прикладное нелинейное программирование» М.: Мир 1975