Реферат: Методи вирішення проблем дискретного логарифмування

Методи вирішення проблем дискретного логарифмування

1. Метод Поліга-Хелмана

Метод Поліга-Хелмана запропонований в 1978 році для визначення дискретного логарифма в мультиплікативній групі поля .

Він заснований на відомій для групи факторизації порядку групи за ступенями простих чисел

Стосовно до адитивної групи точок з генератором порядку маємо Відповідно до відомої китайської теореми про залишки існує єдине натуральне число , таке що

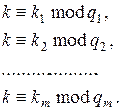
Після визначення значення дискретний логарифм здобувають за допомогою розширеного алгоритму Евкліда. Наведемо приклад.

Приклад 1

Нехай порядок циклічної групи дорівнює , а точка , тобто . Це значення має бути визначене в підсумку рішення ECDLP.

Тут На першому етапі визначаємо точку Отримуємо точку другого порядку з відомими координатами Оскільки , маємо перше порівняння

На наступному етапі знаходимо одну із точок третього порядку Ці точки також відомі, тому з отримуємо наступне порівняння

Нарешті, визначаємо точку 5-го порядку й отримуємо

.

Наведені три порівняння дають єдине розв’язання В загальному випадку необхідно знати координати точок із загальної кількості .

Задача ускладнюється із зростанням переважно простого співмножника в розкладанні порядку групи. У цьому зв'язку для захисту від атаки Поліга-Хелмана порядок криптосистеми обирають рівним великому простому числу, при цьому порядок кривої називають ² майже простим ² (з малим множником ).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--