Реферат: Методи вирішення проблем дискретного логарифмування

й .

У порівнянні з подвоєнням точки (2), яке вимагає обчислення двох множень й інверсії елемента (найбільш трудомістка обчислювальна операція), ділення (5) не вимагає інверсії елемента й може бути реалізоване набагато швидше.

Найбільш ефективне розв’язання рівняння (3) і операцій (4), (5) виконуються в НБ (нормальному базисі) мінімальної складності, зокрема, в ОНБ (оптимальному нормальному базисі).

Розв’язання квадратного рівняння в НБ здійснюється за допомогою простої -бітової рекурентної послідовності. Слід (4) елементів парної ваги дорівнює 0, а непарної ваги - 1.

Піднесення у квадрат (добування кореня квадратного) у нормальному базисі зводиться до циклічного зсуву вправо (вліво) -бітового елемента поля.

Поряд з додаванням елементів за модулем 2 перераховані операції часто називають ²безкоштовними² і не враховують у наближених розрахунках обчислювальної складності. Ділення відповідно до (5) вимагає лише двох множень у нормальному базисі як найбільш складних операцій. Це приблизно на порядок збільшує швидкість виконання операцій ділення на два в порівнянні з операцією подвоєння точки.

Розглянемо можливі підходи до розв’язання задач дискретного логарифма. Найбільш проста ситуація виникає для кривої

,

,

з коефіцієнтом , порядок якої

Максимальний простий порядок досягається при . Покладемо, що , а генератор має порядок . У циклічній групі всі точки є точками подільності на два, відповідно до (4) їх -координати мають слід й, отже, непарну вагу при поданні в НБ. При діленні на два отримуємо дві точки, одна з яких належить групі й має порядок , а інша максимальний порядок

Вони мають відповідно непарну й парну вагу -координат і легко розрізнюються без множення на Вибір однієї із точок (5) порядку здійснюється досить просто. Оскільки в групі випливає, що

то після множення визначається вага елемента або його слід.

При (парна вага елемента) користуються другою формулою (5), у протилежному випадку - першою формулою (5). Таким чином, ділення на два з вибором точки порядку практично зводиться до двох множень у поле.

Відзначимо, що при послідовному діленні на два для половини всіх кривих (з коефіцієнтом і порядком достатнім виявляється лише одне множення в поле.

Для цього при кожному діленні обчислюється лише розв'язання квадратного рівняння (4) і координата точки ділення. Нехай , і при послідовному діленні на два з вибором точки із групи одержуємо

.

Згідно з (5) (перша формула) , . . . , , тому підсумовуючи рівності

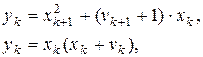
отримуємо з урахуванням першого ділення

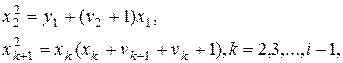(6)

де кожне з рішень вибирається так, щоб виконувалася умова тобто в НБ вагу вектора була непарним.

Як видно, рекурентне обчислення за формулою (6) не вимагає обчислення координати на кожному кроці ділення, замість неї слід лише запам'ятати параметри й . За необхідності – координата обчислюється як

Таким чином, відповідно до (6) алгоритм послідовного ділення на дві точки із групи вимагає лише одного множення елементів у поле . Це чудова властивість операції ділення на два можна використати з метою збільшення продуктивності обчислень як при криптоаналізі, так і при швидкому експоненціюванні будь-якої точки із групи .

Якщо припустити, що для будь-якої точки ми знайшли спосіб визначення парності (непарності) , то послідовна процедура віднімання й ділення на два з вибором точки із групи за поліноміальний час приведе нас до відомої точки .

Значення у двійковому поданні визначається самою процедурою віднімання-ділення. Зрозуміло, що така функція вже не однобічна. Це питання поки залишається відкритим і доводиться вирішувати відомими методами з експонентною складністю.

Для кривої з коефіцієнтом оптимальний порядок . При діленні на дві точки із групи , як й у попередньому випадку, отримуємо дві точки порядку й , однак обидві точки ділення парні й мають слід - координат (і, відповідно, парна вага в нормальному базисі).

Визначити, яка з них має порядок , можна шляхом множення кожної з них на , але це вимагає більших обчислювальних витрат. Більш раціональне дворазове ділення на два, яке в одній з галузей дасть дві точки порядку , вони не діляться на два й мають координати непарної ваги. Ця галузь відбраковується й залишається точка із групи