Реферат: Методичні підходи до обробки ЕЕГ

У випадку відліків дійсних даних одержуємо

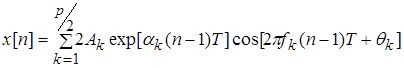. (5)

Якщо число комплексних компонент парне, то матимемо затухаючих синусоїд. Якщо непарне – , затухаючих косинусоїд і одну цілком затухаючу експоненту.

Амплітудний спектр сигналу, розрахований методом Проні, наведений на рис. 3. Видно, що основним недоліком детермінованої моделі є обмежений порядок, пов'язаний з тим, що факторизація характеристичного полінома здійснюється явно. Навіть при використанні удосконалених алгоритмів факторизації максимально досяжний порядок не перевищує 256, що ускладнює виділення спектральних піків для зашумленої вибірки, якою є електроенцефалограма. Таким чином, оптимальними методами спектрального оцінювання в клінічній електроенцефалографії слід вважати статистичні алгоритми на основі АР-моделі.

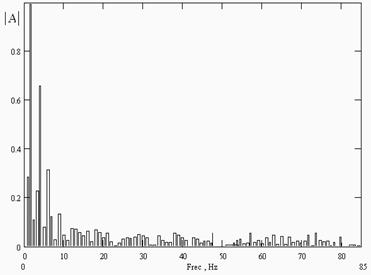
Рисунок 3 – Спектр енергії сигналу, розрахований методом Проні

Проведений аналіз показує можливості комп'ютерних методів аналізу випадкових процесів типу ЕЕГ. Розрахунок спектрів ЕЕГ дозволяє уникнути суб'єктивних помилок, викликаних впливом артефактів і шумів, особливо під час аналізу інтервалів великої тривалості. Порівняння результатів розрахунку спектрів ЕЕГ за допомогою непараметричного методу дискретного перетворення Фур'є і параметричних методів: модифікованого ковариаційного методу та апроксимації за допомогою детермінованої експоненціальної моделі (метод Проні), показує, що найбільш високе частотне розрізнювання ритмів ЕЕГ забезпечується при використанні параметричного авторегресивного методу, який можна рекомендувати під час розробки програмного забезпечення комп'ютерних енцефалографів.

3. Автокореляційна функція (АКФ)

Однією з найважливіших часових характеристик сигналу є АКФ, яка дозволяє судити про ступінь зв'язку (кореляції) сигналу з його зміщеною в часі копією. Для дійсного сигналу , заданого в часі і обмеженого за енергією, автокореляційна функція визначається таким виразом:

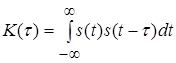. (6)

З формули (6) видно, що при функція автокореляції стає рівною енергії сигналу, і подібність сигналу з його не зміщеною копією максимальна

.

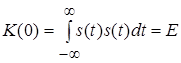Якщо зробити заміну змінних , то одержимо

,

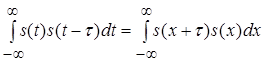звідси виходить така властивість АКФ, як її парність.

Нарешті, важлива властивість функції автокореляції сигналу полягає в тому, що при будь-якому значенні часового зсуву модуль функції автокореляції сигналу не перевищує енергії сигналу:

.

Зі збільшенням функція автокореляції у всіх сигналів, крім періодичних, спадає (не обов'язково монотонно). Отже, функція автокореляції представляється симетричною кривою з центральним максимумом, що завжди позитивний. При цьому, в залежності від виду сигналу , функція автокореляції може мати як монотонно спадаючий, так і коливний характер.

Рис. 4 пояснює побудову функції автокореляції прямокутного імпульсу, що зображений на рис. 4а. На рис. 4б наведена зміщена на (убік відставання) копія сигналу, а на рис. 4в – їхній добуток . Автокореляційна функція для кожного значення чисельно дорівнює площі під кривою добутку імпульсу і його копії, зміщена у часі. Функція автокореляції прямокутного імпульсу має вид трикутника з основою 2, висота якого визначається енергією сигналу (рис. 4г).

Рисунок 4 – Розрахунок функції автокореляції

Для сигналів, що мають нескінченно велику енергією та обмежених за потужністю, автокореляційна функція визначається в одиницях потужності

.

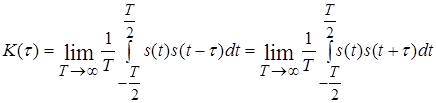Відповідно, значення дорівнює середній потужності сигналу

.

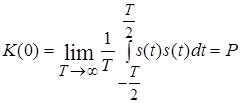При визначенні АКФ періодичної функції усереднення проводиться за її періодом , тобто

.

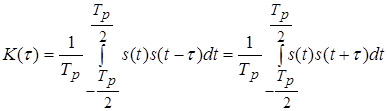Автокореляційна функція періодичного сигналу сама є періодичною функцією з тим самим періодом (рис. 5а).

Дійсно, оскільки періодична функція задовольняє умові , де – період, а , то