Реферат: Методичні вказівки до виконання розрахунко роботи дослідження за допомогою еом коливань системи
1.3. Розкладемо функцію ![]() в ряд Фур’є і визначимо (за допомогою ЕОМ) параметри гармонік в розкладенні.
в ряд Фур’є і визначимо (за допомогою ЕОМ) параметри гармонік в розкладенні.
1.4. Визначимо (за допомогою ЕОМ) рішення ![]() диференціального рівняння руху механичної системи для випадку, коли збурююча сила
диференціального рівняння руху механичної системи для випадку, коли збурююча сила ![]() задається кусочно-лінійною функцією (“точне” рішення).
задається кусочно-лінійною функцією (“точне” рішення).
Розглянемо також випадок, коли сила ![]() задається сумою
задається сумою ![]() гармонік. При цьому встановимо, при якому раціональному значенні
гармонік. При цьому встановимо, при якому раціональному значенні ![]() =
=![]() функція
функція ![]() визначається з 5% точністю (по відношенню до “точного рішення”).
визначається з 5% точністю (по відношенню до “точного рішення”).
Проаналізуємо характер коливального процесу при різних значеннях ![]() <
<![]() .
.
1.5. Користуючись АЧХ и ФЧХ системи та знайденими параметрами гармонік у розкладенні сили ![]() , побудуємо (за принципом суперпозиції) аналітичне рішення
, побудуємо (за принципом суперпозиції) аналітичне рішення ![]() диференціального рівняння, руху механічної системи.
диференціального рівняння, руху механічної системи.
При цьому встановимо, при якому раціональне значені ![]() аналітичне рішення визначається з 5% точністю по відношенню до “точного” рішення.
аналітичне рішення визначається з 5% точністю по відношенню до “точного” рішення.
Співставлення рішень будемо проводити для контрольного моменту часу ![]() , який рекомендується вибирати із умови:
, який рекомендується вибирати із умови:![]() .
.
2. Складання диференціального рівняння вимушених коливань механічної системи.
Рівняння вимушених коливань заданої механічної системи (рис.1) складемо за допомогою рівняння Лагранжа ІІ-го роду:
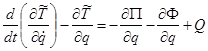 , ( )
, ( )
де ![]() і
і ![]() - узагальнена координата та швидкість,
- узагальнена координата та швидкість, ![]() і
і ![]() - кінетична і потенціальна енергії системи відповідно,
- кінетична і потенціальна енергії системи відповідно, ![]() - функція розсіювання,
- функція розсіювання, ![]() - узагальнена непотенціальна сила.
- узагальнена непотенціальна сила.
Складемо вираз кінетичної енергії системи в її довільному положенні, враховуючи, що тіло 1 виконує поступальний рух, а тіла 2 і 3 – обертальний рух; при цьому швидкості усіх тіл виразимо через узагальнену швидкість ![]() :
:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
 =
=  .
.
У виразі ![]() та
та ![]() - моменти інерції тіл 2 і 3 відносно центральної осі.
- моменти інерції тіл 2 і 3 відносно центральної осі.
Позначимо коефіцієнт ![]() =
=![]() , де
, де ![]() - зведена маса системи. Тоді:
- зведена маса системи. Тоді:
![]()
![]()
![]() . ( )
. ( )
Складемо вираз потенціальної енергії системи: ![]() , де
, де ![]() - потенціальна енергія сил ваги, а
- потенціальна енергія сил ваги, а ![]() - потенціальна енергія сил пружності, що діють на тіла системи.
- потенціальна енергія сил пружності, що діють на тіла системи.
Обчислемо потенціальну енергію системи в її довільному положенні як роботу потенціальних сил на переміщенні системи із довільного положення в положення статичної рівноваги:
![]() ;
;
![]() ,
,
де ![]() ;
; ![]()
![]()
![]() ;
;
тут ![]() ,
, ![]() - статичні подовження пружин;
- статичні подовження пружин; ![]() ,
, ![]() - зміна довжини відповідної пружини при відхиленні системи від стану статичної рівноваги;
- зміна довжини відповідної пружини при відхиленні системи від стану статичної рівноваги; ![]() ,
,![]() - подовження пружини в довільному положенні системи.
- подовження пружини в довільному положенні системи.
Врахуємо, що  ,
, ![]() =
=![]() , а в стані статичної рівноваги
, а в стані статичної рівноваги ![]() .
.
Вираз потенціальної енергії системи та її похідної мають вигляд:
 ;
;
![]() .
.
При рівновазі системи (![]() ) маємо:
) маємо:
![]() , тобто
, тобто ![]() .
.
Тоді вираз потенціальної енергії системи приймає вигляд:
 =
=![]() , ( )
, ( )
де ![]() =
=![]() .
.
Функцію розсіювання ![]() будемо вважати залежною від узагальненої швидкості
будемо вважати залежною від узагальненої швидкості ![]() , а її похідну представимо у вигляді:
, а її похідну представимо у вигляді:
![]() ,
,
де ![]() - коефіцієнт в’язкості (дисипативний коефіцієнт).
- коефіцієнт в’язкості (дисипативний коефіцієнт).
До непотенціальних сил, що діють на систему, відноситься тільки збурююча сила ![]() , можлива робота якої
, можлива робота якої ![]() ; тоді
; тоді
![]() .
.
Візьмемо відповідні похідні і складемо рівняння Лагранжа для заданої системи:
![]()
![]() ;
; 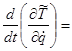
![]() ;
; ![]() 0;
0; ![]()
![]() ;
;
![]() =
=![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() , ( )
, ( )
де ![]() і
і 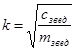 .
.
Диференціальне рівняння ( ) представляє собою неоднорідне диференціальне рівняння другого порядку відносно узагальненої координати ![]() зі сталими коефіцієнтами.
зі сталими коефіцієнтами.
Рішення задачі про дослідження вимушених коливань системи зводиться до рішення цього диференціального рівняння при заданих початкових умовах задачі. Оскільки у розглянутому випадку рух системи починається із стану статичної рівноваги, то початкові умови будуть нульовими:
при ![]() :
: ![]() ;
; ![]() . ( )
. ( )
Як відомо, аналітичне рішення рівняння ( ) складається із суми двох рішень ![]()
![]() , де
, де ![]() - загальне рішення однорідного рівняння,
- загальне рішення однорідного рівняння, ![]() - частинне рішення неоднорідного диференціального рівняння.
- частинне рішення неоднорідного диференціального рівняння.
Слід зауважити, що рішення ![]() в даному випадку (при відповідному підборі коефіцієнта
в даному випадку (при відповідному підборі коефіцієнта ![]() ) практично згасає через
) практично згасає через ![]() . Тоді получається, що при
. Тоді получається, що при ![]()
![]() .
.