Реферат: Методичні вказівки до виконання розрахунко роботи дослідження за допомогою еом коливань системи

== 0,2 + 0 += 0,2 + 0,056 = 0,256т;

== + 10 = 3,56 + 10 = 13,6кН^. м ^–1 ;

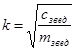
=7,29с ^–1 ; =0,861с;

= 0,456кН^. с^. м ^–1 ;

==0,891с ^–1 .

Для перевірки вірності визначення коефіцієнту рекомендується підрахувати значення співмножника в рішенні при =5^. 0,861 = 4,31с:

.

Таке значення співмножника (наближене до нуля) в рішенні підтверджує факт, що вільні коливання системи на цей момент часу практично згасають; значить коефіцієнт знайдено вірно.

3. Визначення амплітудних- та фазово-частотних характеристик системи.

Шляхом виведення, за допомогою ЕОМ, для заданої механічної системи з параметрами = 0,256т; = 13,6кН^. м ^–1 ; = 0,456кН^. с^. м^–1 получимо (шляхом введення на друкарський пристрій – принтер) амплітудно- та фазово-частотніх характеристики системи та приведемо їх на рис.2 і рис.3 (відповідно).

4. Розкладання функції F(t) в ряд Фур’є та визначення параметрів гармонік збурюючої сили.

Розкладемо функцію в ряд Фур’є:

, ( )

де - номер гармоніки, а - число гармонік в розкладенні.

Визначимо (за допомогою ЕОМ) параметри гармонік: амплітуди , частоти та початкової фази .

Для заданої сили “прямокутного” типу з параметрами кН, значення параметрів гармонік наведені у табл.1.

Таблиця 1.

Номер гармоніки,	, кН	,	, рад.
1	0,764	2	0
2	0,255	6	0
3	0,153	10	0
4	0,109	14	0
5	0,085	18	0

5. Дослідження вимушених коливань механічної системи.

5.1. Визначення (за допомогою ЕОМ) “точного” рішення диференціального рівняння. Аналіз рішення.

Визначимо за допомогою ЕОМ “точне” рішення диференціального рівняння для випадку, коли сила представлена однією гармонікою (=1). Два графіка функцій для відповідних випадків виводяться на екран ЕОМ. Перед виводом графіків на друкарський пристрій їх треба “промасштабувати”, тобто получити рішення на заданому відрізку інтегрування 0, де рекомендується задавати рівним 810. На рис.4 приведені вказані графіки функцій для заданої механічної системи. Лінія 1 відображає “точне” рішення, а лінія 2 – рішення у випадку = 1 (тобто, коли ).

Із графіків видно, що функції получаються періодичними, тобто рух механічної системи получається періодичним-коливальним. І в першому, і в другому випадку при с процеси получилися явно усталеними, тобто без вільних коливань. Але в “точному” рішенні навіть при явно виражені дві частоти – одна дорівнює (див. лінію 2 для випадку = 1; це частота першої гармоніки), а друга частота – втричі більша (це частота другої гармоніки, див. табл. 1). Рішення, що відповідають лініям 1 і 2, значно відрізняються одне від одного. Наприклад, в момент часу с (=4,31с) значення м (точне рішення) і м (випадок = 1).

5.2. Підбір (за допомогою ЕОМ) раціональної кількості гармонік в розкладанні функції .

Визначимо (за допомогою ЕОМ) функції для випадків = 2, 3. На рис. 5, а, б лініями 1 показані графіки для “точного” рішення, а лініями 2 – графіки тих же функцій для випадків = 2; = 3 (відповідно). Із рисунків випливає, що при = 2 графік відрізняється від “точного” рішення, але в значно меншій степені, ніж при = 1. А у випадку = 3 графік практично не відрізняється від “точного” рішення.

Значення відповідних функції при с становлять м (= 2) і м (= 3), тобто при = 2 різниця в значеннях відповідає D = 5,7%, а при = 3 - D = 3,7%.

За одержаним результатам можна зробити висновок, що для отримання рішення з 5% точністю достатньо взяти кількість гармонік = 3 в розкладенні збурюючої сили в ряд Фур’є.

5.3. Побудова аналітичного рішення диференціального рівняння. Підбірраціональної кількості гармонік в розкладанні функції .

Побудуємо аналітичне рішення диференціального рівняння ( ), представивши збурюючу силу розкладенням в ряд Фур’є:

.

Врахуемо, що при рішення практично згасає. Тоді для цих моментів часу:

=. ( ).

Відмітимо, що рішення змінюється з частотою , яка є частотою відповідної гармоніки збурюючої сили.

Користуючись даними табл. 1 та графіками АЧХ і ФЧХ системи, визначимо значення коефіцієнта динамічності та зсуву фаз для

гармонік (), а також амплітуди коливань механічної системи , що відповідають цим гармонікам.

Значення знайдених величин зведемо у табл. 2.

Таблиця 2.

Номер гармоніки,	, с-1			, м	, м	, рад
1	2	0,274	1,08	0,0562	0,0607	0,088
2	6	0,823	2,63	0,0188	0,0497	0,076
3	10	1,37	1,06	0,0113	0,012	3,09
4	14	1,92	0,366	0,008	0,0029	3,09
5	18	2,47	0,195	0,006	0,0012	3,09

Із табл. 2 випливає, що визначальними є амплітуди коливань першої () та другої () гармоніки в рішенні , значення цих амплітуд одного порядку; амплітуди третьої гармоніки () майже в 6 разів менша, а четверта () – в 20 разів менша, ніж амплітуди перших двох гармонік. Цим пояснюється факт виділення частот перших двох гармонік функції в рішенні .

Обмежимося значенням = 3 і побудуємо рішення для випадку усталених вимушених коливань (). Оскільки (табл. 1), рішення має вигляд:

=

= (м).