Реферат: Методика изучения показательной и логарифмической функции в курсе средней школы Простейшие показательные

При любом () и любых положительных x и y, выполнены равенства:

1. log_a 1=0

2. log_a a=1

3. log_a xy= log_a x+ log_a y

4. log_a x/y= log_a x- log_a y

5. log_a x^p = plog_a x

При доказательстве используется основное логарифмическое тождество:

x=a^logax ; y=a^logay

Рассмотрим доказательство 3:

xy=a^logax a ^logay =a^logax+logay т.е. xy=a^logax+logay =a^logaxy , ч.т.д.

Основные свойства логарифма широко применяются в ходе преобразования выражений, содержащих логарифмы.

№497 (Алгебра и начала анализа, 10-11)

Найти , если:

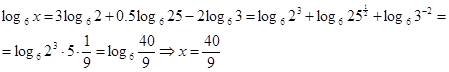
т.е. равны основания логарифмов, равны значения логарифмов равны логарифмируемые выражения. Этот прием рассуждения в дальнейшем будет применим при решении простейших логарифмических уравнений.

З. Понятие обратной функции и методика его введения

Наиболее доступным введение логарифмической функции можно было бы провести после введения понятия обратной функции. Однако методика изложения темы об обратной функции сложна из-за сложных самого материала. Тема "Понятие об обратной функции" приведена в учебнике "Алгебры и начала анализа. 10-11" и рассчитана на необязательное изучение. В эту тему входят:

1) обратимость функций, связанное с решением следующих задач: вычислить значение функции по данному значению аргумента и найти значение аргументов, при которых функция принимает данное значение . Вторая задача не всегда имеет единственное решение (например, для , ). Функция принимает каждое свое значение в единственной точке области определения, называется обратимой, т.е. если обратима, а число принадлежит , то уравнения имеет решение и притом только одно.

2) Обратная функция – как новое понятие – поясняется на конкретных примерах.

Определение. Пусть - произвольная обратимая функция. Для любого числа из ее области значений имеется в точности одно значение , принадлежащее области определения , такое, что: . Поставив в соответствие каждому это значение , получим новую функцию с областью определения и областью значений .

Задача. Найти функцию, обратную функции

Покажем, что уравнения при любом значении имеет единственное решение .

, где .

Если вспомнить область значения данной функции , то получаем положительный ответ. Таким образом, наша функция обратима и обратная ей функция

Алгоритм решения таких задач: найти и данной функции ; поменять местами в формуле переменные , т.е. получить формулу и из полученного равенства выразить через .

В более сложных случаях (когда функция не является обратимой на всей области определения) следует пользоваться теоремой: об обратной функции:

Если функция f возрастает (или убывает) на промежутке I, то она обратима. Обратная к f функция g, определенная в области значений f, также является возрастающей (или убывающей).