Реферат: Методика изучения показательной и логарифмической функции в курсе средней школы Простейшие показательные

x=y² -3y+2=y² -2y*3/2+9/4-9/4+2=(y-3/2)² -ј => (y-3/2)² =x+1/4, где x≥-1/4 => y₁ =3/2+(x+1/4)^1/2 и y₂ =3/2-(x+1/4)^1/2 .

D(y₁ )= D(y₂ )=E(x² -3x+2)=[-1/4;+∞)

Для нахождения областей значений обратных функций обратимся к графику, используя следующее свойство:

Графики функции f и обратной к ней функции g симметричны относительно прямой y=x.

x² -3x+2=0 => x₁ =1; x₂ =2

x_в =3/2; y_в =-1/4

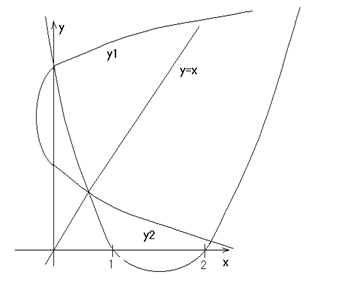
Из графика видно, что

E(y₁ )=[3/2;+∞), E(y₂ )=(-∞;3/2].

4. Методика изучения логарифмической функции, ее свойств и их приложения. Производная показательной и логарифмической функции

Методика изучения логарифмической функции

Изучение логарифмической функции начинается с выделения определения: функцию, заданную формулой называют логарифмической функцией с основанием . Основные свойства выводится из свойств показательной функции:

1. ,

т.к. при решении уравнения

,

т.е. любое положительное число имеет логарифм по основанию .

2. ,

т.к. по определению логарифма любого действительного числа справедливо равенство:

,

т.е. функции вида принимает значение в точке .

3. Логарифмическая функция на всей области определения возрастает (при a>1) или убывает (при 0<a<1).

Покажем, что при a>1 возрастает. Пусть и , надо доказать, что: . Допустим противное, т.е. что . Т.к. показательная функция при a>1 возрастает, то из неравенства следует: , что противоречит выбору . Следовательно: и функция при a>1 – возрастает.

Т.к. при a>1 функция возрастает, то логарифмическая функция положительна при x>1 и отрицательна для 0<x<1 (для основания 0<a<1 – наоборот). На основании рассмотренных свойств строится график этой функции.

Производная показательной и логарифмической функции

Приступая к изучению производной показательной и логарифмической функций, учащиеся знакомятся с новым для них числом e. Необходимость появления этого числа связывается с решением задачи о касательной к графику показательной функции, с угловым коэффициентом, равным 1, т.е. без доказательства принимается следующее утверждение:

существует такое число, больше 2 и меньшее 3 (это число обозначают буквой е), что показательная функция y=e^x в точке 0 имеет производную, равную 1, т.е. (e^Δx -1)/ Δx - при Δx-0.

Теорема: функция e^ж дифференцируема в каждой точке области определения и (e^x )'= e^x . Опр.: Натуральным логарифмом называется логарифмом по основанию е:

ln x = log_e x

Верно соотношение:

e^{ln a} =a => a^x =(e^{ln a} )^x =e^{x ln a} .