Математика / Реферат: Методы и алгоритмы построения элементов систем статистического моделирования

Реферат: Методы и алгоритмы построения элементов систем статистического моделирования

Уравнение Колмогорова-Чепмена относится к классу рекуррентных соотношений, позволяющих вычислить вероятность состояний марковского случайного процесса на любом шаге (этапе) при наличии информации о предшествующих состояниях.

Дальнейшие математические соотношения зависят от конкретного вида марковской цепи.

4.1. Поглощающие марковские цепи

Как указывалось выше, у поглощающих ДМЦ имеется множество, состоящее из одного или нескольких поглощающих состояний.

Для примера рассмотрим переходную матрицу, описывающую переходы в системе, имеющей 4 возможных состояния, два из которых являются поглощающими. Матрица перехода такой цепи будет иметь вид:

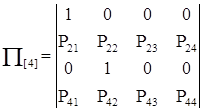(5)

Практически важным является вопрос о том, сколько шагов сможет пройти система до остановки процесса, то есть поглощения в том или ином состоянии. Для получения дальнейших соотношений путем переименования состояний матрицу (8.5) переводят к блочной форме:

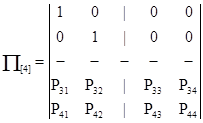(6)

Такая форма позволяет представить матрицу (6) в каноническом виде:

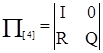(6а)

где 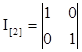- единичная матрица;

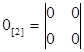- нулевая матрица;

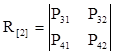- матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество;

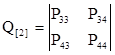- матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний.

На основании канонической формы (6а) получена матрица, называемая фундаментальной:

(7)

В матрице (7) символ (-1) означает операцию обращения, то есть

(8)

После соответствующих преобразований матрица (7) примет вид:

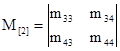(7а)

Каждый элемент матрицы (7а) соответствует среднему числу раз попадания системы в то или иное состояние до остановки процесса (поглощения).

Если необходимо получить общее среднее количество раз попадания системы в то или иное состояние до поглощения, то фундаментальную матрицу М необходимо умножить справа на вектор-столбец, элементами которого будут единицы, то есть

(8а)

где .

Для иллюстрации приведем конкретный числовой пример: пусть известны значения переходных вероятностей матрицы с одним поглощающим состоянием: ; ; ; ; ; ; ; .

Переходная матрица в блочной системе будет выглядеть так:

В данном случае

; ; ;

Проделаем необходимые вычисления:

;

В данном случае компоненты вектора означают, что если процесс начинается с состояния , то общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния , то - 2,26.

В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить слева.

Так, если задать в нашем примере время пребывания в состоянии , а в состоянии - , то общее время до поглощения будет равно:

В случаях, когда марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких - реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей.

Обозначим через вероятность того, что процесс завершится в некотором поглощающем состоянии при условии, что начальным было состояние . Множество состояний снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом: