Реферат: Методы линейного программирования для решения транспортной задачи

ее можно переписать в виде разности двух двойных сумм:

.

Преобразуем эти суммы следующим образом. Первая из них в развернутом виде дает

или

.

Аналогично вторую двойную сумму можно записать так:

.

Тогда равенство запишется в иной форме:

.

Но есть сумма компонент плана по j -му столбцу, она

равна потребности j -ro пункта назначения

.

Аналогично есть сумма компонент плана, взятая по i -й строке, она равна запасам в i -м пункте отправления

.

Эти равенства сумм компонент по строке и столбцу соответственно запасам и потребностям будут выполняться для любого допустимого плана, в том числе и для взятого в самом начале плана Х (x_ij ):

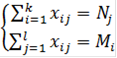
Поэтому для любых допустимых планов будем иметь

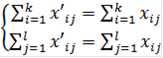
и в написанном выше равенстве суммы x ¢_ij можно заменить соответствующими суммами x_ij :

Теперь вернемся к форме записи

.

В плане Х (x_ij ) по условию его потенциальности для каждой положительной компоненты x_ij > 0 выполняется равенство v_j - u_i = a_ij .

Остальные компоненты плана равны нулю, и соответствующие слагаемые в сумме обратятся в нули. Поэтому полученная сумма будет равна

.

Подставляя в

,

приходим к неравенству