Реферат: Методы моделирования производственных систем

1. По матрице смежности определим ранг каждого элемента

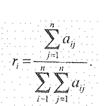
для нашего случая ΣΣaij= 33, Ранги структурных элементов приведены в последнем столбце таблицы 1.

Чем выше ранг элемента, тем более сильно он связан с другими
элементами и тем более тяжелыми будут последствия при потере качества
его функционирования, В нашем случае наиболее высокий ранг (0.12) имеет
четвертый элемент структуры.

2.Проверим связность структуры.

Для связных структур (не имеющих обрывов и висячих элементов) должно выполняться условие

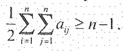Правая часть неравенства определяет необходимое минимальное число
связей в структуре графа, содержащего nвершин.

Для нашего случая n(количество структурных элементов) равно 17и
условие 1/2 33 = 17-1 выполняется, т. е. структура является связной.

3. Проведем оценку структурной избыточности R, отражающей
превышение общего числа связей над минимально необходимым:

где m - множество ребер графа (1/2 количества связей в матрице смежности);

n - количество вершин (элементов) структуры;

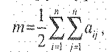где aij- элементы матрицы смежности.

Данная характеристика является косвенной оценкой экономичности и надежности исследуемой структуры и определяет принципиальную возможность функционирования и сохранения связей системы при отказе некоторых ее элементов. Система с большей избыточностью R потенциально более надежна, но менее экономична. Возможны три варианта: если R< 0, то система несвязная; R = 0, система обладает минимальной избыточностью; R> 0, система имеет избыточность; чем выше R, тем выше избыточность.

Для нашего случая R = 33*0.5/(17-1)-1= 0,031, т. е. структура имеет избыточность.

4. Определим неравномерность распределения связей - Е. данный показатель характеризует недоиспользование возможностей данной структуры, имеющей mребер и n вершин, в достижении максимальной связности. Величина Е определяется по формуле

где - вес i-гo элемента, или количество связей i-го элемента со

всеми остальными.

Для нашего случая Е= 3,87.

Однако для сравнения различных структур по неравномерности связей используют относительную величину:

где Е_мах - максимальное значение неравномерности связей, которое достигается в системе, имеющей максимально возможное число вершин, имеющих одну связь.

Величину Е определяют но эмпирической формуле

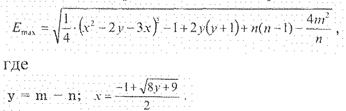
Для нашего случая у- 16.5-17=-0,5; х= 0.615

Тогда Е_{m ах} =14.35

Определим величину Е для нашего случая. Е = 3.84/14.35 = 0.27 Величина Eдля различных типов структур изменяется от 0 (для структур с равномерным распределением связей) до 1,

В нашем случае распределение связей в структуре довольно равномерное.

5. Определим структурную компактность структуры Q, которая отражает общую структурную близость элементов между собой. Для этого используем формулу
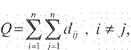