Реферат: Методы предварительных эквивалентных преобразований и итерационные методы с минимизацией невязки для решения СЛАУ

Реферат « Введение в численные методы »

Тема: «Методы предварительных эквивалентных преобразований и итерационные методы с минимизацией невязки для решения СЛАУ»

1. Методы предварительных эквивалентных преобразований

1.1 Преобразование вращения

Следующий важный подход к решению алгебраических систем уравнений базируется на применении эквивалентных преобразований с помощью унитарных матриц, сводящем исходную матрицу к эквивалентной ей диагональной.

Смысл этого подхода состоит в том, чтобы последовательно, умножением слева и / или справа на специальные унитарные матрицы, превратить некоторые компоненты исходной матрицы в нуль.

Матрица S называется унитарной, если ее произведение со своей комплексно сопряженной равно единичной матрице. Это означает, что комплексно сопряженная матрица равна обратной матрице:

Известной унитарной матрицей является матрица вращения ,которая применяется для поворота на заданный угол вектора, принадлежащего некоторой плоскости, вокруг начала координат. В двумерном случае вектор поворачивается на угол путем умножения на матрицу

Чтобы сохранить эквивалентность результирующей матрицы при умножении ее на матрицу вращения, необходимо исходную матрицу умножать справа на и слева на . Умножение же матрицы вращения на вектор дает такой же по величине вектор, но повернутый на заданный угол.

Поворот вектора в многомерном пространстве на произвольный угол можно представить, как последовательность плоских вращений каждой проекции на некоторый угол. Если подобрать угол вращения так, чтобы в плоском повороте одну из проекций вектора совместить с координатной осью, то вторая проекция в этой плоскости становится равной нулю.

Частные повороты вектора в многомерном пространстве с помощью матрицы вращения можно выполнять, если ее расширить до матрицы размера следующим образом:

.

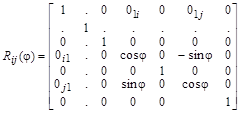Индексы i, j обозначают матрицу вращения, поворачивающую вектор в плоскости на угол .

Теперь частное эквивалентное преобразование матрицы A вращением на угол записываются так:

.

Условие превращения в нуль ij- тых элементов симметричной матрицы A можно получить методом неопределенных коэффициентов на двумерной матрице:

.

.

Угол поворота, при котором , находится из уравнения

.

Разделив на и обозначив , , получим квадратное уравнение для тангенса требуемого угла поворота

.

Из двух решений для тангенса выбирается такое, чтобы . В этом случае . Подставив выражение для угла в соотношения для диагональных элементов, после тригонометрических преобразований получаются следующие формулы:

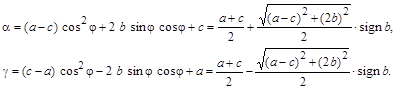
Для получения результирующей матрицы выполнять матричное умножение трех матриц совсем необязательно. Структура матриц вращения вызывает при умножениях изменение только тех элементов исходной матрицы, которые находятся на i- той и j- той строчках и на i- том и j- том столбцах. Изменения представляются суммами элементов, стоящих в строчках и столбцах, умноженных на синус или косинус угла в соответствии с формулами, где j>i :

преобразования строк – ;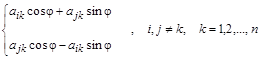

преобразование столбцов –.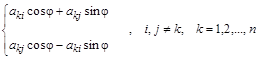

На пересечениях i -й строки и i- того столбца и j -й строки и j- того столбца располагаются соответственно вычисленные выше и , а на местах ij -того и ji -того элементов вставляются нули.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--