Реферат: Методы предварительных эквивалентных преобразований и итерационные методы с минимизацией невязки для решения СЛАУ
1.2 Ортогональные преобразования отражением
Следующей важной унитарной матрицей, с помощью которой в различных алгоритмах выполняются ортогональные преобразования, являются матрицы отражения. Использование этого инструмента позволяет, например, последовательными эквивалентными преобразова-ниями свести исходную матрицу к верхней треугольной (QR-алгоритмы), трех или двух диагональным и т.д.
Смысл этого подхода состоит в том, чтобы умножением матрицы A слева на специально подобранную унитарную матрицу ![]() один из столбцов исходной матрицы (например,
один из столбцов исходной матрицы (например, ![]() ) преобразовать в вектор, параллельный единичному координатному вектору
) преобразовать в вектор, параллельный единичному координатному вектору ![]() (
(![]() или
или ![]() ). Тогда, последовательно подбирая нужные унитарные матрицы
). Тогда, последовательно подбирая нужные унитарные матрицы ![]() и соответствующие единичные векторы
и соответствующие единичные векторы ![]() , после n циклов эквивалентных преобразований можно будет получить верхнюю треугольную матрицу:
, после n циклов эквивалентных преобразований можно будет получить верхнюю треугольную матрицу:
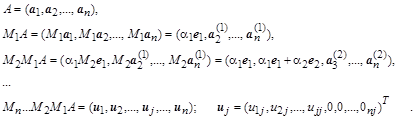
При выборе в качестве начального вектора ![]() и умножениях матрицы A на ортогональные матрицы справа в конечном счете можно получить нижнюю треугольную матрицу.
и умножениях матрицы A на ортогональные матрицы справа в конечном счете можно получить нижнюю треугольную матрицу.
Весь вопрос состоит в том, как формировать унитарную матрицу с заданными свойствами из векторов ![]() и столбцов
и столбцов ![]() матрицы A .
матрицы A .
Из аналитической геометрии известно, что любые векторы, лежащие в плоскости, взаимно перпендикулярны с ее нормалью, т.е. их проекции на нормаль равны нулю. Последнее эквивалентно равенству нулю скалярных произведений.
Чтобы (k+ 1) – мерный векторный треугольник ![]() сделать параллельным k- мерной гиперплоскости с нормалью n (вектор единичной длины, перпендикулярный плоскости), необходимо приравнять нулю скалярное произведение: (n , y )=0.
сделать параллельным k- мерной гиперплоскости с нормалью n (вектор единичной длины, перпендикулярный плоскости), необходимо приравнять нулю скалярное произведение: (n , y )=0.
Пусть вектор z не параллелен плоскости, заданной своей нормалью, тогда его проекции на эту плоскость и нормаль соответственно будут представлены векторами ![]() и
и ![]() . Вектор z и вектор зеркально-симметричный ему
. Вектор z и вектор зеркально-симметричный ему ![]() через эти проекции можно выразить так:
через эти проекции можно выразить так:
![]()
Разрешив первое относительно ![]() и подставив его в
и подставив его в ![]() , получим
, получим
![]()
Проекцию вектора ![]() можно заменить скалярным произведением (n , z ) и подставить в выражение для
можно заменить скалярным произведением (n , z ) и подставить в выражение для ![]() , выразив тем самым зеркально отраженный вектор через исходный вектор и нормаль гиперплоскости:
, выразив тем самым зеркально отраженный вектор через исходный вектор и нормаль гиперплоскости:
![]()
Здесь M представляет унитарную матрицу, преобразующую произвольный вектор в зеркально отраженный. В том, что матрица унитарная, нетрудно убедиться, проверив ее произведение со своей комплексно сопряженной:
![]()
Выражение для зеркально отраженного вектора позволяет представить нормальный вектор в виде линейной функции от задаваемого вектора z :
![]()
Число ![]() в знаменателе является нормирующим множителем. Нормальный вектор представляющий гиперплоскость обязан иметь единичную длину. Коэффициент
в знаменателе является нормирующим множителем. Нормальный вектор представляющий гиперплоскость обязан иметь единичную длину. Коэффициент ![]() , который в общем случае является комплексным числом, необходимо выбрать так, чтобы скалярное произведение
, который в общем случае является комплексным числом, необходимо выбрать так, чтобы скалярное произведение ![]() было больше нуля. Если учесть соотношение для согласованных норм:
было больше нуля. Если учесть соотношение для согласованных норм: ![]() , то
, то
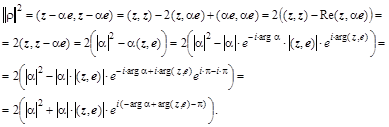
Выбрав ![]() для комплексных матриц или
для комплексных матриц или ![]() – для действительных матриц, будем иметь
– для действительных матриц, будем иметь
![]()
Такое нормирование не нарушает коллинеарности отраженного и единичного векторов:
![]()
![]()
Рассмотрим пример воздействия ортогонального преобразования на матрицу
 .
.

